filmov
tv
What is a Group Action? : A Group as a Category and The Skeleton Operation ☠
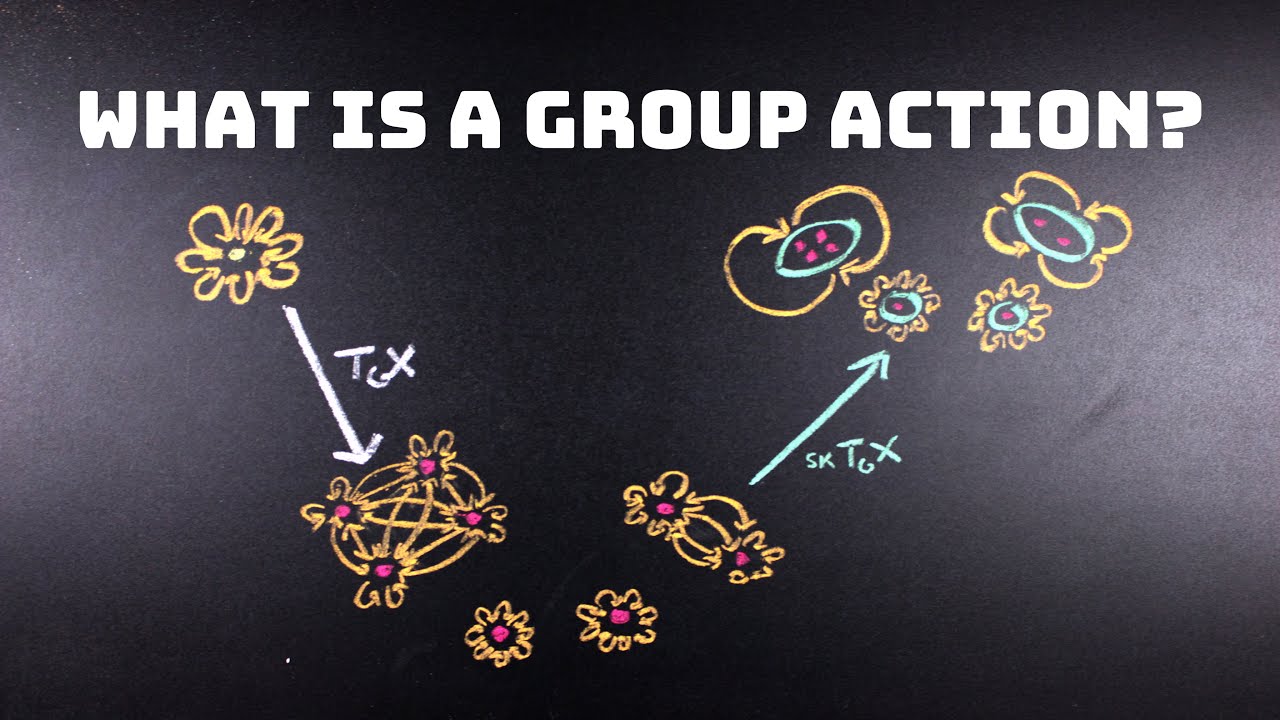
Показать описание
This week I try to take a more Categorical approach to answering and expanding upon the question of "what is a group action". Along the way I'll go over thinking about a group as a category and eventually hit on the skeleton operation on a category and use it to present an example of the categorification of the Orbit-Stabilizer theorem. Here are some videos that are "pre-reqs", that is, they introduce some topics in a bit more detail than I do here.
CORRECTIONS:
1. When introducing Groups, while glossing over the group axioms I forget to mention that a group, G, must be closed under the binary operation. That is for any a,b in G, ab must also be in G.
This video can be broken up into the following sections.
00:00 Intro
I once again fail to say "Hi I'm Nathan and Welcome to my YouTube Channel" but I still introduce the goal of the video lol.
00:32 What is a Group Action?
I briefly revisit the idea of what a group is before "complicating" it into the object that we'll spend most of the time interacting with, a group action. There are many different types of group actions but we will focus on 2 examples.
03:46 Example 1
The first of 2 group action examples. We look at probably the most accessible example of a group action, a group acting on itself with the action operating the same way as the group operation.
05:05 Example 2
In the second of 2 group action examples we look at another small but more complicated example of a group acting on itself, here we us the conjugate action and we'll continue to look at this example throughout the video.
After the second example, the video begins to bring in a lot more ideas from category theory and we'll spend a lot of time looking at categories and groups and how the two can correspond to one another.
09:30 A Group as a Category
Here I will begin translating the idea of what we have talked about with groups and group actions into a more category theoretic context. We won't dive too deep into the Category of G-Sets, but we do define what G-Sets are and how they can be described as functors.
11:21 The Translation Groupoid of A Group
Next we 'zoom in' on what our G-Set functor does to the categorical group and arrive at the directed graphs that we looked at previously by looking at the Translation Groupoid.
13:27 The Skeleton Operation
The last Category theoretic tool we will need for the categorification of the orbit-stabilizer theorem, the skeleton operator on a category fuses together identical (or isomorphic) objects, which allows us to see the information in the Translation Groupoid category more clearly.
15:50 The Orbit-Stabilizer Theorem
Here we introduce (not prove...) the theorem and then talk through how the skeleton operation on the translation groupoid generates a very nice picture of the theorem in a Category Theoretic context.
17:35 Another way of Thinking about the Skeleton Category
And lastly I pull away from the abstract nonsense of the skeleton construction to quickly walk through another way to interpret each of the orbits in the skeleton category that can help when trying to determine the size of other symmetry/dihedral groups.
_____________________
_____________________
WHAT GEAR I USED FOR THIS VIDEO:
DISCLAIMER: Links included in this description may be affiliate links. If you purchase a product or service with the links that I include here, I may receive a small commission. There is no additional charge to you! Thank you for supporting my channel and for helping me create these free videos!
Subscriber Count as of release: 1,783
#CHALK #CategoryTheory #Skeleton
CORRECTIONS:
1. When introducing Groups, while glossing over the group axioms I forget to mention that a group, G, must be closed under the binary operation. That is for any a,b in G, ab must also be in G.
This video can be broken up into the following sections.
00:00 Intro
I once again fail to say "Hi I'm Nathan and Welcome to my YouTube Channel" but I still introduce the goal of the video lol.
00:32 What is a Group Action?
I briefly revisit the idea of what a group is before "complicating" it into the object that we'll spend most of the time interacting with, a group action. There are many different types of group actions but we will focus on 2 examples.
03:46 Example 1
The first of 2 group action examples. We look at probably the most accessible example of a group action, a group acting on itself with the action operating the same way as the group operation.
05:05 Example 2
In the second of 2 group action examples we look at another small but more complicated example of a group acting on itself, here we us the conjugate action and we'll continue to look at this example throughout the video.
After the second example, the video begins to bring in a lot more ideas from category theory and we'll spend a lot of time looking at categories and groups and how the two can correspond to one another.
09:30 A Group as a Category
Here I will begin translating the idea of what we have talked about with groups and group actions into a more category theoretic context. We won't dive too deep into the Category of G-Sets, but we do define what G-Sets are and how they can be described as functors.
11:21 The Translation Groupoid of A Group
Next we 'zoom in' on what our G-Set functor does to the categorical group and arrive at the directed graphs that we looked at previously by looking at the Translation Groupoid.
13:27 The Skeleton Operation
The last Category theoretic tool we will need for the categorification of the orbit-stabilizer theorem, the skeleton operator on a category fuses together identical (or isomorphic) objects, which allows us to see the information in the Translation Groupoid category more clearly.
15:50 The Orbit-Stabilizer Theorem
Here we introduce (not prove...) the theorem and then talk through how the skeleton operation on the translation groupoid generates a very nice picture of the theorem in a Category Theoretic context.
17:35 Another way of Thinking about the Skeleton Category
And lastly I pull away from the abstract nonsense of the skeleton construction to quickly walk through another way to interpret each of the orbits in the skeleton category that can help when trying to determine the size of other symmetry/dihedral groups.
_____________________
_____________________
WHAT GEAR I USED FOR THIS VIDEO:
DISCLAIMER: Links included in this description may be affiliate links. If you purchase a product or service with the links that I include here, I may receive a small commission. There is no additional charge to you! Thank you for supporting my channel and for helping me create these free videos!
Subscriber Count as of release: 1,783
#CHALK #CategoryTheory #Skeleton
Комментарии
 0:10:51
0:10:51
 0:20:53
0:20:53
 0:04:35
0:04:35
 0:09:02
0:09:02
 0:21:58
0:21:58
 0:24:53
0:24:53
 0:06:07
0:06:07
 0:20:19
0:20:19
 0:55:00
0:55:00
 0:08:34
0:08:34
 0:17:43
0:17:43
 0:06:56
0:06:56
 0:14:27
0:14:27
 0:20:19
0:20:19
 0:29:48
0:29:48
 0:07:15
0:07:15
 0:11:02
0:11:02
 0:32:35
0:32:35
 0:12:27
0:12:27
 0:11:22
0:11:22
 0:07:23
0:07:23
 0:06:23
0:06:23
 0:41:51
0:41:51
 0:44:05
0:44:05