Chapter 7: Group actions, symmetric group and Cayley’s theorem | Essence of Group Theory

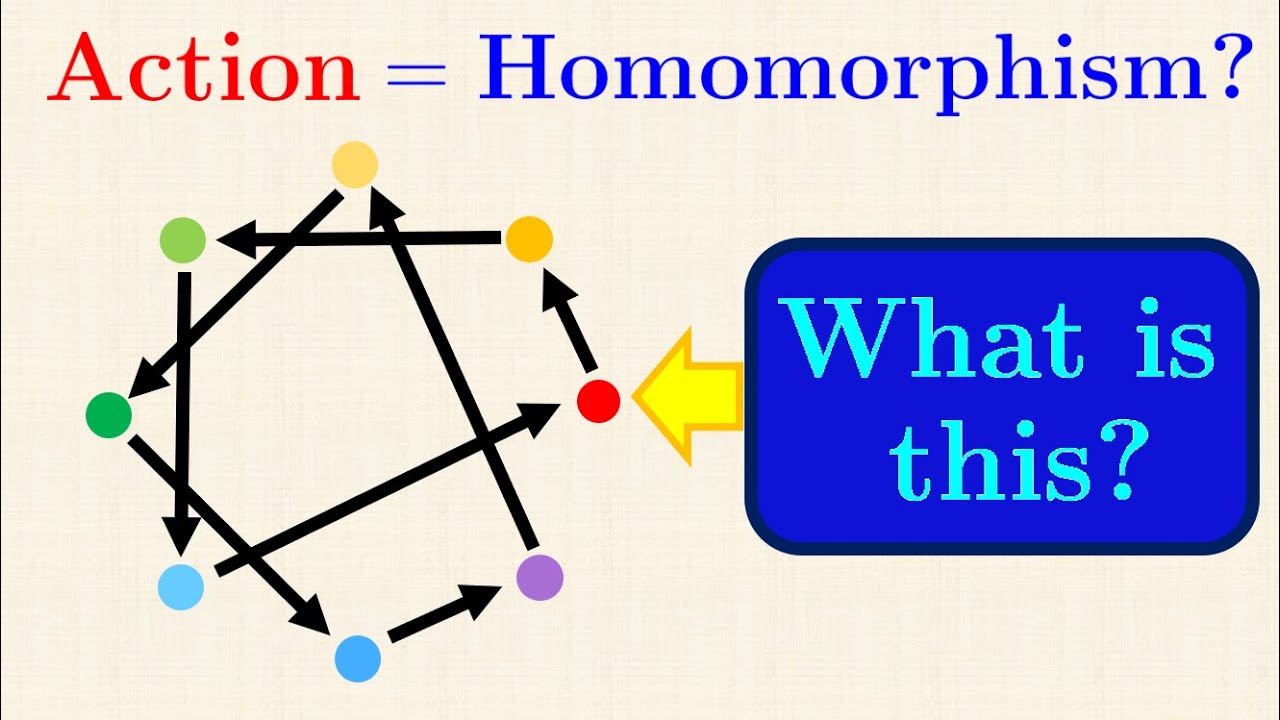
Group action can be thought of as a homomorphism to a symmetric group, so apart from orbit-stabiliser theorem, we can also use the isomorphism theorem to analyse any group action. It turns out that this correspondence between group action and homomorphism can be visualised rather easily. This correspondence is very important in group theory, but often neglected.

Symmetric group is also briefly mentioned here as a concept to facilitate the introduction of the above correspondence, but a more detailed analysis of the symmetric group would not be in this video series, because I don't think it is as intuitive as concepts discussed in the video series and therefore does not fit the theme of the series too well. However, I will do a video on Burnside's lemma and its interesting application, but it is not "Essence of Group Theory" anymore, because it is an application of the orbit-stabiliser theorem. I haven't mentioned in the video that I will also not do a video on matrix groups because it requires the knowledge of linear algebra, and again, the concepts discussed in the matrix groups will usually be algebraic.

The next few videos will be a summary of this video series with one very cool example that really covers all the concepts discussed in this video series; another video on the current epidemic explaining an alternative model to the SIR discussed on this channel before, and will be about a stochastic branching process; then the Burnside's lemma video. There might be some videos in between these, but I will definitely do all of these videos in some time in the future.

Cayley's theorem is named in honour of Arthur Cayley, a British (Cambridge) mathematician who is also known for a lot of mathematical results, like Cayley table, Cayley graph, Cayley's theorem and the famous Cayley-Hamilton theorem in linear algebra. However, even though it is a motivation for the study of symmetric groups, you might not see Cayley's theorem too often in more advanced studies of group theory. It mainly acts as a direct application of the correspondence discussed in this video.

Other than commenting on the video, you are very welcome to fill in a Google form linked below, which helps me make better videos by catering for your math levels:

If you want to know more interesting Mathematics, stay tuned for the next video!

SUBSCRIBE and see you in the next video!

If you are wondering how I made all these videos, even though it is stylistically similar to 3Blue1Brown, I don't use his animation engine Manim, but I will probably reveal how I did it in a potential subscriber milestone, so do subscribe!

#mathemaniac #math #grouptheory #groupaction #homomorphism #Cayley

Social media:

[mathemaniac]

This time, when I say "a few days", it really means a short time. It should be exactly 1 week from now, which is way more frequent than my recent schedule... will strive to make more videos in the summer!
This will help me make better videos by making them more catered for the viewers!

[jgy]

It's kinda sad that everything at some point eventually ends, but putting that aside, this was a very interesting series, for me at least, it motived myself to actually start studying abstract algebra, so thanks for that! As for suggestions, I would love seeing something like a "'Essence of Ring Theory" as a follow-up for this series, I personally love ring, even more than group, so I'd like to see your take on them.

[samuelefraizzoli]

I'm so glad and grateful that there is such wonderful material on the Internet.
All your videos are of exceptional quality and a source of thoughtful inspiration, even if the topic is more or less known (I'm a physicist).
Best regards
Samuele

[gooomaaal]

very insightful. for first time I can distinguish between symmetry and permutation.

[michellehobdari]

Thank you so much for this series, the animations were very clear and well explained - it saved my essay!

[nainamat]

Your explanations in the videos are excellent ! Plzz make videos on types of group actions 😊

[hamzakeurti]

This series was so enjoyable to watch, any chance you would elaborate on group actions on some future chapter? And relationship to manifolds?

[JoJoModding]

The symmetric group actually is a symmetry, namely all the ways you can permute the variables of symmetric functions in n variables while preserving the function value.

[hyperduality]

The image (co-domain) is a copy, equivalent or dual to the factor group (domain) - the 1st isomorphism theorem.
Isomorphism is dual to homomorphism.
Injective is dual to surjective synthesizes bijective or isomorphism.

[LemoUtan]

How might one go about animating essences of this thing called 'group character' I wonder?

[noahsegal]

Would it be possible to make a video explaining the Abel-Ruffini theorem?

[barbietripping]

1:35 thank you for reassuring my understanding regarding swapping the vertices. Is there a link to topology to be made here, since the resulting figure has a different number of regions?

[toaj]

Is the homomorphism from the group of symmetries to the symmetric group always an injection?

[tac]

Thank you for your Video.
In Japan, there are few books which has a lot of pictures because the price should be about 2, 000 to 3, 000 yen, the students can buy it.
They usually take class of Math.
So, it is not good for me to study by myself. I don't know why they sell the kind of books in store but only in university.
Anyway, picture is important to understand.
Thank you.