filmov
tv
Homomorphisms and Isomorphisms -- Abstract Algebra 8

Показать описание
⭐Support the channel⭐
⭐my other channels⭐
⭐My Links⭐
⭐my other channels⭐
⭐My Links⭐
Isomorphisms (Abstract Algebra)
Homomorphisms (Abstract Algebra)
Group Homomorphisms - Abstract Algebra
Group Homomorphism and Isomorphism
The Kernel of a Group Homomorphism – Abstract Algebra
Intro to Group Homomorphisms | Abstract Algebra
Homomorphisms and Isomorphisms -- Abstract Algebra examples 8
Homomorphisms and Isomorphisms -- Abstract Algebra 8
Chapter 6: Homomorphism and (first) isomorphism theorem | Essence of Group Theory
Abstract Algebra Lectures Part 3: Homomorphisms and Isomorphisms
Abstract Algebra | First Isomorphism Theorem for Groups
Abstract Algebra | Ring homomorphisms
Abstract Algebra 1.2 : Isomorphisms and Homomorphisms
Abstract Algebra | Group homomorphisms
Ring Homomorphisms and Isomorphisms -- Abstract Algebra 21
Isomorphic Groups and Isomorphisms in Group Theory | Abstract Algebra
Proof: Basic Properties of Homomorphisms (Identities and Inverses) | Abstract Algebra
Abstract Algebra - 10.1 Group Homomorphisms and Properties
Abstract Algebra 10.4: Homomorphisms and Kernels
Abstract Algebra Homomorphisms First Isomorphism Theorem
Isomorphism
Ring homomorphisms and isomorphisms -- Abstract Algebra Examples 21
Homomorphism And Isomorphism|Abstract Algebra - Part 2
Introduction to homomorphism
Комментарии
 0:05:04
0:05:04
 0:04:12
0:04:12
 0:10:04
0:10:04
 0:06:03
0:06:03
 0:04:53
0:04:53
 0:15:01
0:15:01
 0:17:17
0:17:17
 0:53:59
0:53:59
 0:12:47
0:12:47
 0:23:26
0:23:26
 0:15:35
0:15:35
 0:20:01
0:20:01
 0:11:30
0:11:30
 0:17:13
0:17:13
 1:02:52
1:02:52
 0:13:58
0:13:58
 0:05:57
0:05:57
 0:18:03
0:18:03
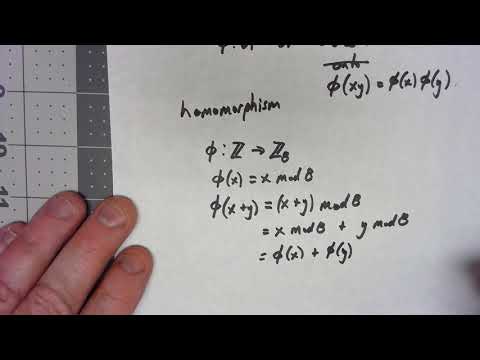 0:07:50
0:07:50
 0:07:37
0:07:37
 0:12:51
0:12:51
 0:32:40
0:32:40
 0:13:36
0:13:36
 0:14:31
0:14:31