filmov
tv
Let y=y(x) be the solution curve JEE Main 2024 (Online) 8th April Evening Shift

Показать описание
Solve this Question:
Let y=y(x) be the solution curve of the differential equation secy dy/(" " dx)+2xsiny=x^3 cosy,y(1)=0. Then y(√3) is equal to:
A π/6
B π/12
C π/3 JEE Main 2024 (Online) 8th April Evening Shift
D π/4
PDF Solution -
Follow Us on Social Media
Stay connected with us on social media for updates, study tips, and more:
Facebook:
/ dkacademyiit
Instagram:
/ dkacademy_official
🌐Website:
ccess the complete playlist of Quadratic Equations
• Quadratic equation
Complete PYQ Chapter Wise
1) Quadratic Equations :- • Quadratic equation
2) Straight Lines :- • STRAIGHT LINE .
3) Limits Continuity and Differentiability :- • Limits continuity and Differentiability
Mastering Continuity PYQ Sections for IIT JEE Mathematics with DK Sir
Welcome to an in-depth exploration of Differential Equations PYQ (Previous Year Questions) Calculus Sections in IIT JEE Mathematics, guided by the renowned DK Sir. In this comprehensive video, we delve into the critical concepts, techniques, and problem-solving strategies required to ace the IIT JEE exams, specifically focusing on continuity sections.
Introduction to differential equations Calculus Sections
calculus sections are a fundamental topic in the IIT JEE Mathematics syllabus. Understanding parabolas is crucial for solving complex mathematical problems efficiently. In this video, DK Sir breaks down the concepts in a clear and concise manner, ensuring that students grasp the fundamentals before moving on to more advanced problems.
Why differential equation calculus Sections are Important for IIT JEE
Parabolas, as part of conic sections, form a significant portion of the IIT JEE Mathematics curriculum. They are frequently tested in the exam, making it essential for students to have a strong command over this topic. Mastering parabola conic sections not only boosts your confidence but also enhances your overall performance in the Mathematics section of the IIT JEE exam.
Previous Year Questions (PYQ) Analysis
Step-by-step solutions to previous year IIT JEE questions on Continuity calculus sections.
Tips and tricks for solving complex problems quickly and accurately.
Benefits of Learning with DK Sir
Expert Guidance: DK Sir is an experienced IIT JEE Mathematics tutor with a deep understanding of the exam pattern and question types. His teaching methods are tailored to help students grasp complex concepts with ease.
Clear Explanations: Each topic is explained in a simple and straightforward manner, making it easy for students to follow along and understand.
Time Management Tips: Learn how to manage your time effectively during the exam to maximize your score in the Mathematics section.
Downloadable PDF Notes: Comprehensive notes covering all the key points discussed in the video.
Practice Worksheets: Extra practice problems to reinforce your understanding of parabola conic sections.
Mock Tests: Simulated IIT JEE Mathematics mock tests to help you gauge your preparation level.
Join Our Community
Subscribe to our YouTube channel for more videos on IIT JEE Mathematics . Join our community of dedicated students and educators who are committed to achieving excellence in the IIT JEE exams. Don’t forget to hit the notification bell to stay updated on our latest videos and live sessions.
Keywords: IIT JEE Mathematics, differential equations, DK Sir, Previous Year Questions, IIT JEE Preparation, Form:
Form: (d^2 y)/(dx^2 )+p dy/dx+qy=g(x)
Homogeneous Equations:
Linear Homogeneous: (d^2 y)/(dx^2 )+p dy/dx+qy=0
Characteristic Equation: Solve r^2+pr+q=0 to find the general solution.
Non-Homogeneous Equations:
Particular Solution: Use methods such as undetermined coefficients or variation of parameters to find a particular solution when g(x)≠0.• Solve first-order and second-order differential equations.
• Apply various solution techniques to solve differential equations.
• Interpret the solution in the context of physical problems or geometrical contexts
JEE Tips, IIT JEE Exam, Mathematics PYQ, IIT JEE 2024, IIT JEE Study Material, IIT JEE Mock Tests, IIT JEE Practice Problems.
#DifferentialEquations #IITJEE #IITJEEMathematics #MathsForIITJEE #JEEPrep MathsInEngineering #JEEStudy #DifferentialEquationsJEE
#iitjee #iit2024 #jee #iit #jeemains #jeeadvanced #jeemain #cbse #education #engineering #aiims #student #exam #science #iitcoaching #exams #kota #iitjeeonline #neetpreparation #iitbombay #iitjeepreparation #iitmain #iitdelhi #pcm #iitmains #mathematics #topper #iitcoach #kotacoaching #iitadvanced #results #main #neetcoaching #advanced #iitadvance #iitresult
Let y=y(x) be the solution curve of the differential equation secy dy/(" " dx)+2xsiny=x^3 cosy,y(1)=0. Then y(√3) is equal to:
A π/6
B π/12
C π/3 JEE Main 2024 (Online) 8th April Evening Shift
D π/4
PDF Solution -
Follow Us on Social Media
Stay connected with us on social media for updates, study tips, and more:
Facebook:
/ dkacademyiit
Instagram:
/ dkacademy_official
🌐Website:
ccess the complete playlist of Quadratic Equations
• Quadratic equation
Complete PYQ Chapter Wise
1) Quadratic Equations :- • Quadratic equation
2) Straight Lines :- • STRAIGHT LINE .
3) Limits Continuity and Differentiability :- • Limits continuity and Differentiability
Mastering Continuity PYQ Sections for IIT JEE Mathematics with DK Sir
Welcome to an in-depth exploration of Differential Equations PYQ (Previous Year Questions) Calculus Sections in IIT JEE Mathematics, guided by the renowned DK Sir. In this comprehensive video, we delve into the critical concepts, techniques, and problem-solving strategies required to ace the IIT JEE exams, specifically focusing on continuity sections.
Introduction to differential equations Calculus Sections
calculus sections are a fundamental topic in the IIT JEE Mathematics syllabus. Understanding parabolas is crucial for solving complex mathematical problems efficiently. In this video, DK Sir breaks down the concepts in a clear and concise manner, ensuring that students grasp the fundamentals before moving on to more advanced problems.
Why differential equation calculus Sections are Important for IIT JEE
Parabolas, as part of conic sections, form a significant portion of the IIT JEE Mathematics curriculum. They are frequently tested in the exam, making it essential for students to have a strong command over this topic. Mastering parabola conic sections not only boosts your confidence but also enhances your overall performance in the Mathematics section of the IIT JEE exam.
Previous Year Questions (PYQ) Analysis
Step-by-step solutions to previous year IIT JEE questions on Continuity calculus sections.
Tips and tricks for solving complex problems quickly and accurately.
Benefits of Learning with DK Sir
Expert Guidance: DK Sir is an experienced IIT JEE Mathematics tutor with a deep understanding of the exam pattern and question types. His teaching methods are tailored to help students grasp complex concepts with ease.
Clear Explanations: Each topic is explained in a simple and straightforward manner, making it easy for students to follow along and understand.
Time Management Tips: Learn how to manage your time effectively during the exam to maximize your score in the Mathematics section.
Downloadable PDF Notes: Comprehensive notes covering all the key points discussed in the video.
Practice Worksheets: Extra practice problems to reinforce your understanding of parabola conic sections.
Mock Tests: Simulated IIT JEE Mathematics mock tests to help you gauge your preparation level.
Join Our Community
Subscribe to our YouTube channel for more videos on IIT JEE Mathematics . Join our community of dedicated students and educators who are committed to achieving excellence in the IIT JEE exams. Don’t forget to hit the notification bell to stay updated on our latest videos and live sessions.
Keywords: IIT JEE Mathematics, differential equations, DK Sir, Previous Year Questions, IIT JEE Preparation, Form:
Form: (d^2 y)/(dx^2 )+p dy/dx+qy=g(x)
Homogeneous Equations:
Linear Homogeneous: (d^2 y)/(dx^2 )+p dy/dx+qy=0
Characteristic Equation: Solve r^2+pr+q=0 to find the general solution.
Non-Homogeneous Equations:
Particular Solution: Use methods such as undetermined coefficients or variation of parameters to find a particular solution when g(x)≠0.• Solve first-order and second-order differential equations.
• Apply various solution techniques to solve differential equations.
• Interpret the solution in the context of physical problems or geometrical contexts
JEE Tips, IIT JEE Exam, Mathematics PYQ, IIT JEE 2024, IIT JEE Study Material, IIT JEE Mock Tests, IIT JEE Practice Problems.
#DifferentialEquations #IITJEE #IITJEEMathematics #MathsForIITJEE #JEEPrep MathsInEngineering #JEEStudy #DifferentialEquationsJEE
#iitjee #iit2024 #jee #iit #jeemains #jeeadvanced #jeemain #cbse #education #engineering #aiims #student #exam #science #iitcoaching #exams #kota #iitjeeonline #neetpreparation #iitbombay #iitjeepreparation #iitmain #iitdelhi #pcm #iitmains #mathematics #topper #iitcoach #kotacoaching #iitadvanced #results #main #neetcoaching #advanced #iitadvance #iitresult
 0:07:04
0:07:04
 0:03:47
0:03:47
 0:00:33
0:00:33
 0:03:12
0:03:12
 0:07:59
0:07:59
 0:02:03
0:02:03
 0:02:45
0:02:45
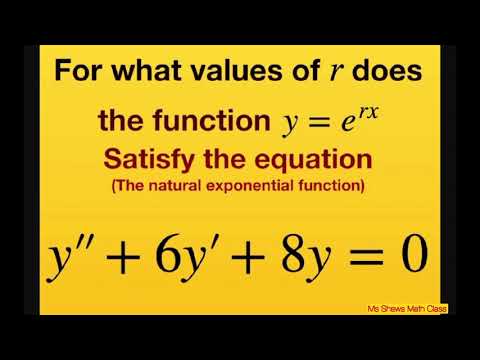 0:02:54
0:02:54
 0:13:57
0:13:57
 0:13:09
0:13:09
 0:10:52
0:10:52
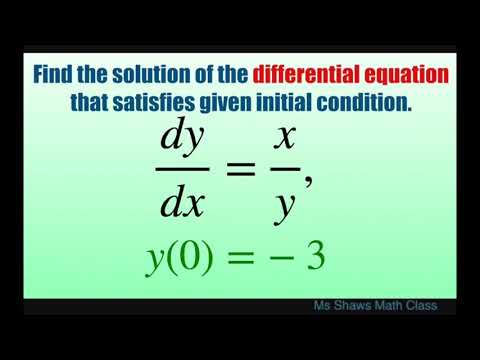 0:02:43
0:02:43
 0:01:47
0:01:47
 0:02:21
0:02:21
 0:00:12
0:00:12
 0:06:48
0:06:48
 0:03:49
0:03:49
 0:00:58
0:00:58
 0:14:31
0:14:31
 0:08:16
0:08:16
 0:25:41
0:25:41
 0:19:45
0:19:45
 0:21:44
0:21:44
 0:03:32
0:03:32