filmov
tv
Super Popular Problem
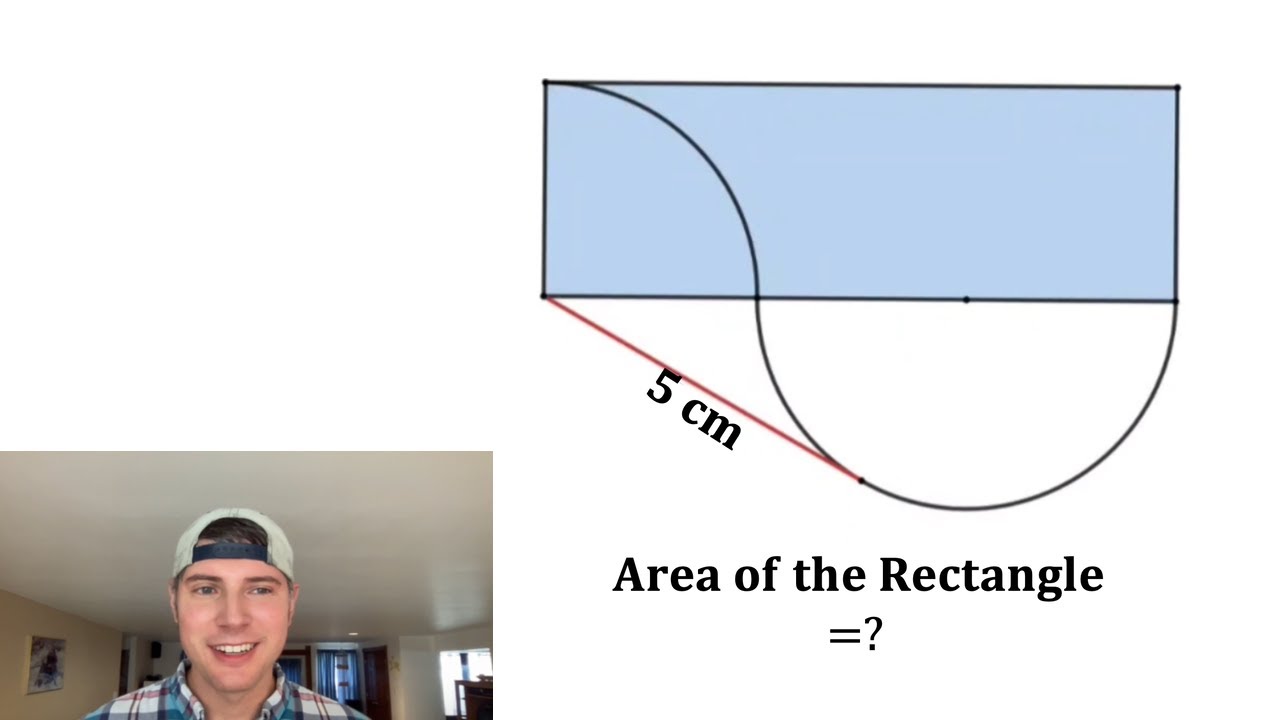
Показать описание
A lot of people sent me requests to go over this problem. I hope you love it!
Super Popular Problem
Popular Math Problem
Absolute Value Equation Challenge
Common Problem | Ep 01 | Marzuk Russell | Shahnaz Khushi | Chashi Alam | Pavel | Drama Serial 2024
Eu Virei o Mais Popular do Servidor!
Common Problem | Ep 02 | Marzuk Russell | Shahnaz Khushi | Chashi Alam | Pavel | Drama Serial 2024
How to solve any problem of world's most popular problems in full details
LG G4 boot loop (the most popular problem) | 1/3 | xSolution
The Weekly Listen: Does Facebook Actually Have a Young Person Problem, the Interactive Ads of the...
Most Popular Love Stars 2 || Size is no problem for Acting
Anyone else have this problem | The Most Popular TikToks of 2021 | New TikTok Dance #shorts
Best 20 Quotes about Problem Solving | Beautiful Quotes | Most Popular Quotes
Anyone else have this problem | The Most Popular TikToks of 2021 | New TikTok Dance #shorts
The MOST popular PROBLEM in Hot Wheels...
The most popular problem of a person who crochet 🙌 #crochettutorial
YouTube’s Most Popular Problem: EXPLAINED!
most popular tricky riddle-logical math puzzle-find the value-problem|| solution||reasoning question
Most popular problem in aeroports #edit #instagram #tiktok #vfx #3d #cgi #effects #istanbul
Top Most popular problem ceiling Fan. Ceiling fan most problem low speed @SkillNagariTi
Production ENDS - why no-one is buying one of Europe's most popular EVs
LPS: The Popular Problem {Short Film}
O no problem is the most popular kids to the
TOP 20 Quotes about Problem ~ Everyday Quotes ~ Most Popular Quotes ~ Happiness Quotes
The most popular areas problem from the channel of Russian youtuber Boris Trushin #maths #math
Комментарии
 0:02:17
0:02:17
 0:01:29
0:01:29
 0:01:16
0:01:16
 0:22:45
0:22:45
 0:47:21
0:47:21
 0:21:00
0:21:00
 0:05:17
0:05:17
 0:03:31
0:03:31
 0:34:17
0:34:17
 0:01:10
0:01:10
 0:00:13
0:00:13
 0:05:21
0:05:21
 0:00:13
0:00:13
 0:00:42
0:00:42
 0:00:11
0:00:11
 0:02:08
0:02:08
 0:01:50
0:01:50
 0:00:09
0:00:09
 0:02:41
0:02:41
 0:06:33
0:06:33
 0:14:53
0:14:53
 0:00:08
0:00:08
 0:04:47
0:04:47
 0:00:43
0:00:43