filmov
tv
A Nice Equation

Показать описание
🤩 Hello everyone, I'm very excited to bring you a new channel (SyberMath Shorts).
Enjoy...and thank you for your support!!! 🧡🥰🎉🥳🧡
If you need to post a picture of your solution or idea:
#numbertheory #exponentials #exponent #diophantineequations
via @YouTube @Apple @Desmos @NotabilityApp @googledocs @canva
PLAYLISTS 🎵 :
Enjoy...and thank you for your support!!! 🧡🥰🎉🥳🧡
If you need to post a picture of your solution or idea:
#numbertheory #exponentials #exponent #diophantineequations
via @YouTube @Apple @Desmos @NotabilityApp @googledocs @canva
PLAYLISTS 🎵 :
The Most Beautiful Equation in Math
A Nice Algebra Problem | Math Olympiad | Solve for a , b?
A Nice Exponential Equation | Math Olympiads
A Nice Exponential Equation
A Nice Math Olympiad Exponential Equation 3^x = X^9
A Nice Diophantine Equation
A nice differential equation
A Nice Exponential Equation | Math Olympiads
Japanese 🇯🇵 |A Nice Olympiad Exponential Problem | Math Olympiad Questions 📘✍️
A Nice Diophantine Equation
a nice integral equation.
Solving A Nice Functional Equation
A Nice Equation with Integer Solutions
A Nice Homemade Exponential Equation
A Nice Exponential Equation
A Nice Equation To Solve | A Nice Algebra problem | Can you solve?
A Nice Exponential Equation
The Most Wholesome Math Equation
a nice iterated floor equation.
not {linear, separable, exact}, but solvable -- a nice differential equation.
Solving a Nice Diophantine Equation in Three Ways
Your Daily Equation #11: Euler's Identity or The Most Beautiful of all Equations
A Nice Algebra Problem | Math Olympiad | How to solve for x ?
Solving a Nice Rational Equation in Two Ways
Комментарии
 0:03:50
0:03:50
 0:15:13
0:15:13
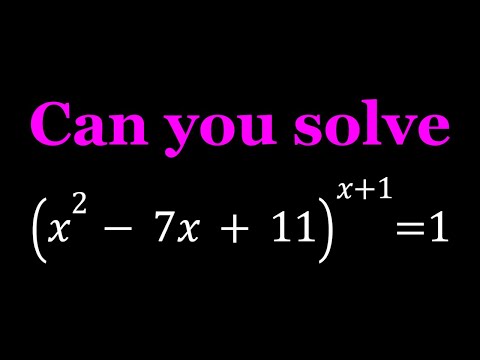 0:09:02
0:09:02
 0:08:50
0:08:50
 0:02:34
0:02:34
 0:08:56
0:08:56
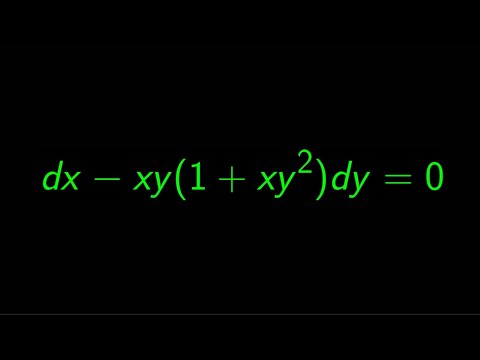 0:06:13
0:06:13
 0:06:50
0:06:50
 0:05:43
0:05:43
 0:08:57
0:08:57
 0:10:44
0:10:44
 0:09:50
0:09:50
 0:07:34
0:07:34
 0:05:31
0:05:31
 0:09:32
0:09:32
 0:03:23
0:03:23
 0:00:48
0:00:48
 0:00:16
0:00:16
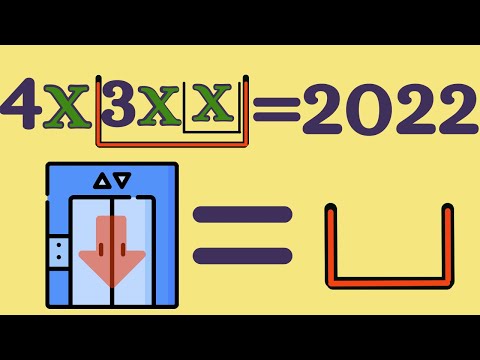 0:06:52
0:06:52
 0:04:43
0:04:43
 0:08:13
0:08:13
 0:26:20
0:26:20
 0:12:27
0:12:27
 0:09:53
0:09:53