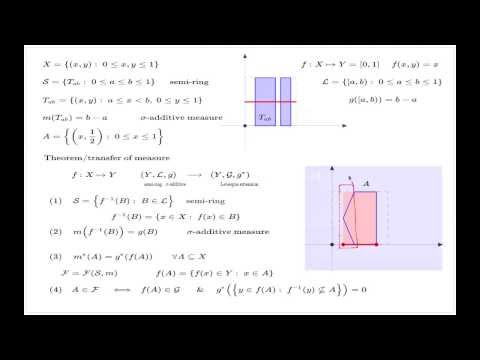
Measure Theory 15 | Image measure and substitution rule

Please consider to support me if this video was helpful such that I can continue to produce them :)

🙏 Thanks to all supporters! They are mentioned in the credits of the video :)

This is part 15 of 22 videos.

#MeasureTheory
#Analysis
#Integral
#Calculus
#Measures
#Mathematics
#Probability

I hope that this helps students, pupils and others. Have fun!

(This explanation fits to lectures for students in their first and second year of study: Mathematics for physicists, Mathematics for the natural science, Mathematics for engineers and so on)

[mirak]

Thank you for your time and your efforts

[alzero]

4:02 is the exact moment a key concept in PhD-level Probability clicked for me, danke!

[SpokewTheBoss]

I like a lot the series, maybe i am missing product measurable spaces.
Thank you for your good explanations and your clear demonstrations.

[metalore]

Self note: sigma finite defined in Part 12. Density function mentioned in parts 13 and 14.

[MrOvipare]

Hey, I heard that naughty bird chirping at 1:50 !
Pay attention little bird, no chatting in the classroom! :)

[duckymomo]

Oh this is change of variables! Now I get it

[rogierbrussee]

If for a measurable map F: X -> Y and a measurable function g:Y -> IR we define the _pullback_  

(F^*g)(x) = (g o F)(x) = g (F(x)) 

then the substitution rule is 

\int_X (F^*g)(x) µ(dx) = \int_Y g(y) (F_*\mu)(dy)

or a bit more abstract the projection formula

g F_* \mu = F_* (F^*g \mu)

[qschroed]

Can this be used to explain that the jacobian is used when converting bounds when integrating multivariable functions?

[nonamemark]

Is it possible yo purchase the pdf files for this specific course? The monthly schedule wouldn't work for me. If possible, pls let me know about the price

[diobrando]

Is this substitution the one we need to use in order to justify the change from dP to dx when working with a continuous cumulative distribution function in probability theory?

[vassillenchizhov]

How is this reconciled with the formula for change of variables in multiple dimensions? For example if we have the invertible and continuously differentiable map h:D->M, where D is a box in R^m and where M is an m-manifold embedded in R^n? Then the derivative of h is a linear map, so it's not clear how to integrate it to get mu_F. Would we then instead define the Lebesgue-Stieltjes measure as \mu_F(A) = \int_A F'(x)dx, but now F' is the square root of the Gramian formed by the derivatives of h: G_{ij} = <\partial_i h, \partial_j h> similar to what we do for integration on manfilods? Do we still write \mu_F = h_{*}\mu = \mu \circ h^{-1} in that case? Is there some specific notation that relates h and F there, or do we just omit F in general and only write dh_{*}\mu when we integrate?

[OnlyOnePlaylist]

Hey, I don't understand how you write the "on the other hand" integral at 10:40 with respect to the measure \mu_F, I don't remember how it is defined this way, you just state that "it has a density of F'(x)dx"

[Fastsina]

Sir, at 8:04, the notation just points to the use of function F as direct or inverse, would a notation mu_F-1 be consistent with the definition of Lebesgue-Stieltjes of the other video but in this case , since we also add a surjective condition ? Or did I mistake the meaning of mu_F

[abdellaziizhb]

where is the proof of Radon-Nikodym and Lebesgue's decomposition theorem please ?