filmov
tv
Integral of ∫sec^3(x)dx
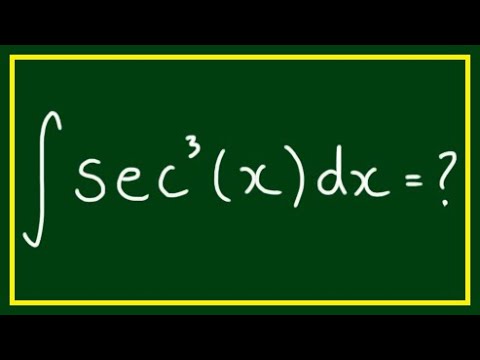
Показать описание
Integrals of odd powers of sec(x) are never straight forward, unlike their even powered counterparts. They get exponentially more difficult as the odd power increases. The integral of sec^3(x) is a classic integral that is still manageable by conventional analytical methods.
Probably the most straight forward approach is to use integration by parts. To do this, we can write the integral as:
∫sec^3(x)dx = ∫sec(x)*sec^2(x)dx
So now we have the 2 parts required for I.B.P. if we let
u = sec(x) and dv = sec^2(x)dx
Please watch the video to see how this integral is solved.
Suggested videos:
Thanks for watching. Please give me a "thumbs up" if you have found this video helpful.
Please ask me a maths question by commenting below and I will try to help you in future videos.
Probably the most straight forward approach is to use integration by parts. To do this, we can write the integral as:
∫sec^3(x)dx = ∫sec(x)*sec^2(x)dx
So now we have the 2 parts required for I.B.P. if we let
u = sec(x) and dv = sec^2(x)dx
Please watch the video to see how this integral is solved.
Suggested videos:
Thanks for watching. Please give me a "thumbs up" if you have found this video helpful.
Please ask me a maths question by commenting below and I will try to help you in future videos.
 0:07:01
0:07:01
 0:06:05
0:06:05
 0:07:36
0:07:36
 0:09:20
0:09:20
 0:04:10
0:04:10
 0:04:26
0:04:26
 0:02:47
0:02:47
 5:47:36
5:47:36
 0:11:24
0:11:24
 0:04:38
0:04:38
 0:02:01
0:02:01
 0:03:50
0:03:50
 0:06:13
0:06:13
 0:08:26
0:08:26
 0:05:00
0:05:00
 0:03:19
0:03:19
 0:09:16
0:09:16
 0:01:37
0:01:37
 0:02:40
0:02:40
 0:00:51
0:00:51
 0:12:41
0:12:41
 0:00:43
0:00:43
 0:02:16
0:02:16