filmov
tv
sec^3 x tan x dx, Evaluate the indefinite integral.
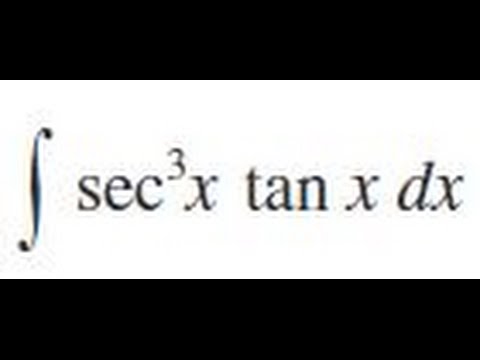
Показать описание
sec^3 x tan x dx, Evaluate the indefinite integral.
Evaluate the Integral sec^3 x tan x dx with substitution rule
sec^3 x tan x dx, Evaluate the indefinite integral.
Integral of tan^3(x)*sec(x), calculus 2 tutorial
Integral of tan^3x, with tan and sec
Integral of sec^3x
Evaluate the Integral tan x sec^3 x dx U-Substitution.
Integral of tan(x)
integral tan(3x) sec(3x) dx , secante por tangente
Class 12th – Integral of tan x dx | Integrals | Tutorials Point
trig integrals involving secant and tangent (calculus 2)
Class 12th – Integral of Tanx Tan2x Tan3x dx | Integrals | Tutorials Point
Evaluate the Integral tan^5 x sec^3 x dx U-Substitution. Example 24. Trigonometric
Evaluate the Integral tan^3 x sec x dx U-Substitution. Example 25. Trigonometric
integral of sec x tan x dx
Integral of tan^3x*sec^4x (read pinned comment)
Integral of sec(x) but without that trick!
Integral of sec(x)
Integral of tanx
Integral of sec^2(x)tan^3(x) dx
integral of x*tan^ -1(x), calculus 2 tutorial, integration by parts
7-30 Evaluate the indefinite integral. ∫^3 x tanx d x
my favorite calculus 2 trigonometry integral (two results off by a constant)
Class 12th – Integral of sec x dx | Integrals | Tutorials Point
when calculus students use trig identities too early
Комментарии
 0:02:40
0:02:40
 0:02:40
0:02:40
 0:02:46
0:02:46
 0:07:01
0:07:01
 0:02:05
0:02:05
 0:02:54
0:02:54
 0:01:14
0:01:14
 0:02:39
0:02:39
 0:16:51
0:16:51
 0:03:29
0:03:29
 0:04:25
0:04:25
 0:02:21
0:02:21
 0:02:48
0:02:48
 0:04:17
0:04:17
 0:12:41
0:12:41
 0:02:16
0:02:16
 0:05:28
0:05:28
 0:00:25
0:00:25
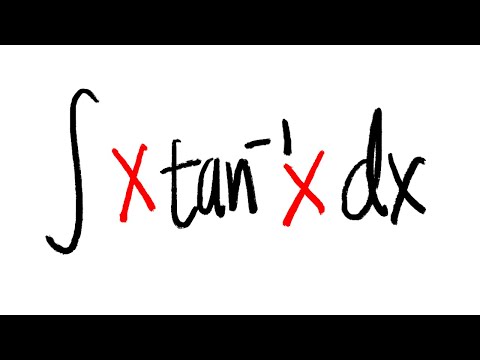 0:05:04
0:05:04
 0:00:33
0:00:33
 0:07:05
0:07:05
 0:02:46
0:02:46
 0:00:43
0:00:43