filmov
tv
1 minute integral vs. 9 minutes integral, trig sub, calculus 2 tutorial

Показать описание
Learn trig substitution with this calculus tutorial! We will go over the integral of sqrt(9-x^2) and the integral of sqrt(9-x^2) from -3 to 3.
----------------------------------------
#blackpenredpen #math #calculus #apcalculus
----------------------------------------
#blackpenredpen #math #calculus #apcalculus
1 minute integral vs. 9 minutes integral, trig sub, calculus 2 tutorial
How REAL Men Integrate Functions
Understand Calculus in 1 minute
Visualizing Integrals
A Year's Worth of Calculus in 1 Minute
One Minute Integral | The AQAL Model #shorts
Understand Calculus in 35 Minutes
Hard Integral with Trig Substitution in UNDER 1 MINUTE! #Shorts
'LEAKED Content Marketing Secrets: 9 AI Tools The 1% Are Hiding!
ALL OF Calculus 2 in 5 minutes
THE ONE MINUTE INTEGRAL: MIT Integration Bee 2011 #3
One Minute Integral | The Integral Movement #shorts
Hard Trig Integral in UNDER 1 MINUTE! #Shorts
81 Math Symbols Explained
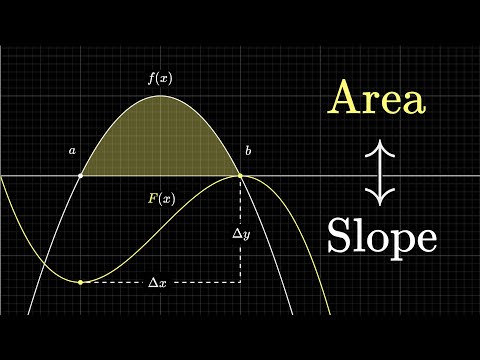
What does area have to do with slope? | Chapter 9, Essence of calculus
Calculus 2: Integration (1 of 9) What is an Integral? What is Integration?
🔥 POV: Integration - Look at me! 👀 💪 | JEE 2024 | Math | Bhoomika Ma'am
Integration and the fundamental theorem of calculus | Chapter 8, Essence of calculus
Why is a Circle 360 Degrees, Why Not a Simpler Number, like 100?
Differentiation and integration important formulas||integration formula
Solving a meme integral in under 1 min.
integral 1 / √(9 + x²) dx
Baby calculus vs adult calculus
How much does a PHYSICS RESEARCHER make?
Комментарии
 0:10:32
0:10:32
 0:00:35
0:00:35
 0:00:57
0:00:57
 0:01:16
0:01:16
 0:01:09
0:01:09
 0:00:57
0:00:57
 0:36:22
0:36:22
 0:00:59
0:00:59
 0:08:18
0:08:18
 0:06:09
0:06:09
 0:01:29
0:01:29
 0:01:00
0:01:00
 0:00:59
0:00:59
 0:08:13
0:08:13
 0:12:39
0:12:39
 0:07:15
0:07:15
 0:00:48
0:00:48
 0:20:46
0:20:46
 0:03:54
0:03:54
 0:00:16
0:00:16
 0:00:52
0:00:52
 0:01:55
0:01:55
 0:00:27
0:00:27
 0:00:44
0:00:44