filmov
tv
Four squares with constant area | Visual Proof | Squaring the segments |
Показать описание
==Hello everyone==
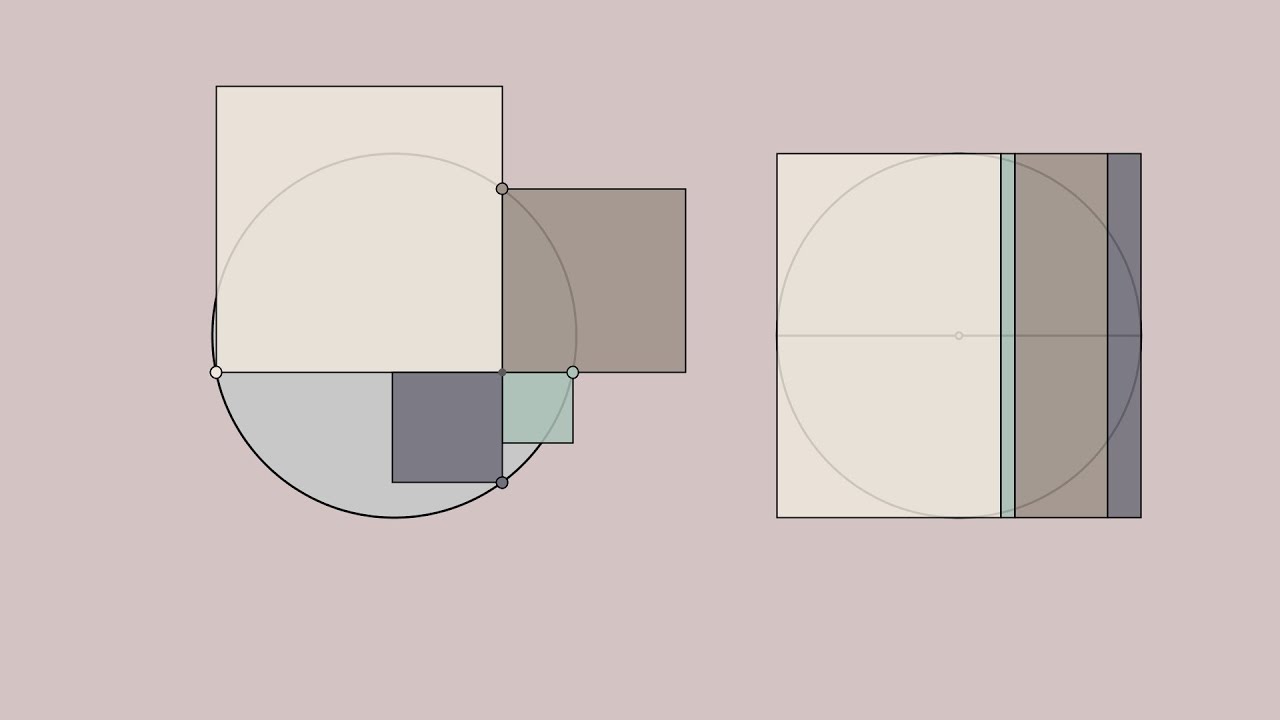
Another visualization and a proof of some simple euclidean geometry. I think it's pretty neat :)
Two chords of a circle intersecting at 90 degrees make up 4 segments. The squares of these 4 segments always add up to the diameter squared. Hope the video is clear and understandable.
Quick update:
We made it over 2k subs! Thanks everyone for all the comments and support. I wouldn't be here without your help and other bigger YouTubers that help me out along the way.
_________________________________________________________________
You can also support me on:
_________________________________________________________________
Any further questions or ideas:
_________________________________________________________________
Programs used:
- Processing
- Adobe Premiere Pro
_________________________________________________________________
MUSIC:
Cellophane Roses - Reaching
Another visualization and a proof of some simple euclidean geometry. I think it's pretty neat :)
Two chords of a circle intersecting at 90 degrees make up 4 segments. The squares of these 4 segments always add up to the diameter squared. Hope the video is clear and understandable.
Quick update:
We made it over 2k subs! Thanks everyone for all the comments and support. I wouldn't be here without your help and other bigger YouTubers that help me out along the way.
_________________________________________________________________
You can also support me on:
_________________________________________________________________
Any further questions or ideas:
_________________________________________________________________
Programs used:
- Processing
- Adobe Premiere Pro
_________________________________________________________________
MUSIC:
Cellophane Roses - Reaching
0:01:56
Four squares with constant area | Visual Proof | Squaring the segments |
0:15:19
Sum of Four Squares
0:05:01
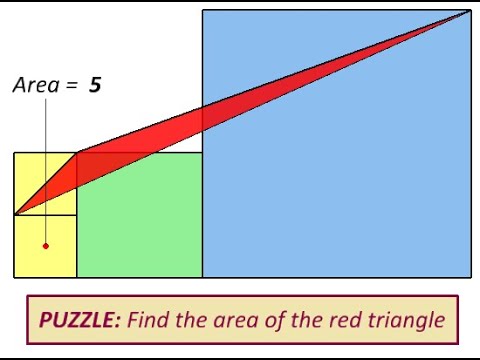
Puzzle Area of Triangle Defined by 4 Squares
0:39:05
Lagrange's Four Squares Theorem
0:06:15
11 2 Sums of Four Squares
0:02:39
The Sum Of The Area Of Four Squares is 2019, Then What Would Be The Area Of The Red Rectangle ?
0:17:08
Why is pi here? And why is it squared? A geometric answer to the Basel problem
0:05:09
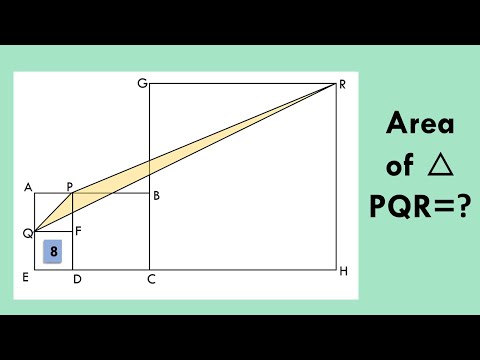
A triangle PQR is placed amid squares; find the area of the yellow triangle PQR
0:11:32
Stats - 3-4 Calculating the Least-Squares Regression Line
0:01:48
Factoring using difference of two squares to a power of 4
0:07:39
Sum of four squares | BSC MATH |
0:14:23
Magic Squares (4x4) & Tests of Divisibility.
0:01:00
Sum of squares of distances from a point on the incircle of an equilateral triangle to its vertices
0:00:59
Using Perfect Squares to Simplify Radical Expressions
0:12:36
Regression and Least Squares | Chapter 4 Applied Linear Algebra
0:22:10
How to Find Area | Rectangles, Squares, Triangles, & Circles | Math Mr. J
0:03:11
Factor completely 81x^4 - 16. Difference of squares. Factor 4a^2 +12ab +9b^2 -25c^2
0:33:49
Least Squares Lecture 4 17 20
0:04:42
Domain and range of Function where Sum of Squares is Constant
0:07:40
Solve by Completing the Square: Step-by-Step Technique
0:49:51
9. Four Ways to Solve Least Squares Problems
0:38:33
Pythagoras twisted squares: Why did they not teach you any of this in school?
0:03:35
Week 20 Higher C 4 Difference of 2 squares and triple bracket
0:10:43
Solving a quadratic by completing the square
Комментарии