filmov
tv
But WHY Does This Pattern Occur? Beauty of Numbers
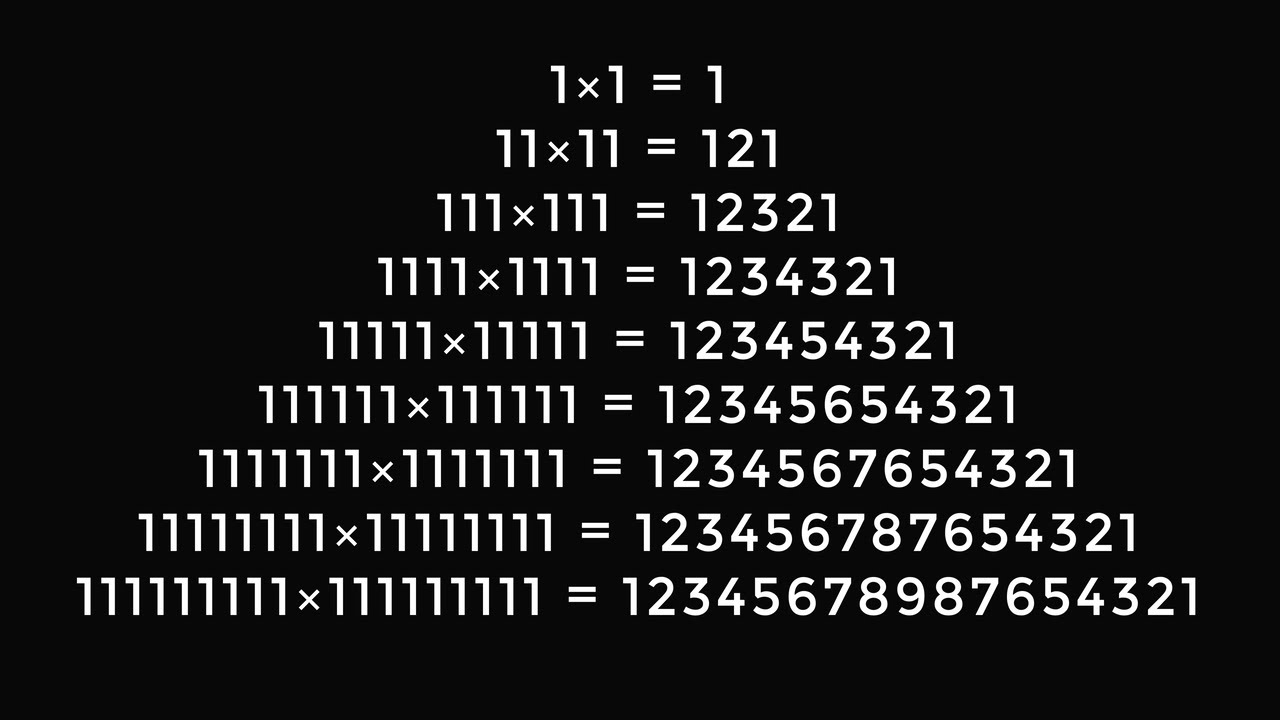
Показать описание
If you multiply a number with only 1s by itself, you end up with a palindrome of the numbers in ascending and then descending order. People have called this an example of the "beauty of mathematics." If your number has N digits of 1, then its square will be the numbers 1 to N in ascending and then descending order. The pattern continues indefinitely, although it "breaks" after 9 because of carry over. I explain why the pattern happens using the method of multiplying by lines.
Connect on social media. I update each site when I have a new video or blog post, so you can follow me on whichever method is most convenient for you.
My Books
Connect on social media. I update each site when I have a new video or blog post, so you can follow me on whichever method is most convenient for you.
My Books
But WHY Does This Pattern Occur? Beauty of Numbers
The Infinite Pattern That Never Repeats
The Pattern to Prime Numbers?
The Most Accurate Harmonic Pattern Indicator For Scalping ( +1340% IN PROFIT )
Watch For These Market Patterns This Week
How To Tell If You Have Pattern Hair Loss (In 15 Seconds)
The Visitor Pattern Explained and Implemented in Java | Behavioral Design Patterns | Geekific
Best Simple Candlestick Pattern For Any Market (Forex, Stocks, Or Crypto)
Left Hand: Caron Easy Crochet Extra Lemon Stitch Baby Blanket Pattern
Doji candle | Types of Doji candlestick | Doji candlestick pattern | Doji candlestick strategy
My best kept sewing pattern secret!
Strumming Pattern for Piano
ESSENTIAL STRUMMING PATTERN YOU MUST KNOW.
There is a pattern in everything | Jason Meisel | TEDxPineCrestSchool
Stop Using Commercial Patterns, Learn Pattern Drafting Instead
This candlestick pattern entry works great
The simple pattern that makes it SOUND like Moonlight Sonata
Double Bottom Chart Pattern | Bullish Reversal Pattern | Chart patterns
ULTIMATE Head And Shoulders Pattern Trading Course (PRICE ACTION MASTERY)
My Favorite Reversal Pattern for Massive Trends
The pleasure of poetic pattern - David Silverstein
Head and Shoulders Chart Pattern | Head and Shoulders Pattern | Bearish Reversal Pattern
How To Unlock Pattern lock on Android
How to make my curl pattern start at the root - Curly wavy hair styling tips!
Комментарии
 0:08:13
0:08:13
 0:21:12
0:21:12
 0:16:27
0:16:27
 0:08:50
0:08:50
 0:27:07
0:27:07
 0:00:40
0:00:40
 0:05:46
0:05:46
 0:00:57
0:00:57
 0:22:06
0:22:06
 0:00:59
0:00:59
 0:00:13
0:00:13
 0:00:25
0:00:25
 0:00:28
0:00:28
 0:10:09
0:10:09
 0:12:31
0:12:31
 0:01:00
0:01:00
 0:00:36
0:00:36
 0:00:56
0:00:56
 0:31:04
0:31:04
 0:00:56
0:00:56
 0:04:47
0:04:47
 0:01:00
0:01:00
 0:03:23
0:03:23
 0:00:29
0:00:29