filmov
tv
Preparation for math olympiad UKMT junior senior intermediate maths challenge smc jmc imc 2022 2023

Показать описание
For learning more ideas send message to my Whatsapp number 00989395025223
UKMT Maths Challenges: A Beginner's Guide - Every Competition Explained
Quick and Easy Technique | Junior Math Olympiad Training
How to prepare for math competitions! Prof. Po Shen Lo
How to Prepare for Math Competitions
He won 4 gold medals in the International Math Olympiads: tips and tricks
Senior Maths Challenge UKMT | Math Olympiad Training
Can You Solve This? | Junior Math Olympiad Training
Russia | Math Olympiad Question | You should know this trick!!
Luxembourg - Math Olympiad Question | You should know this trick
Norway Math Olympiad Question | You should be able to solve this!
What is the UKMT Junior Maths Challenge and how can you prepare?
UKMT tips 2021 | Combinatorics | Intermediate Maths Olympiad Preparation
Preparation for math olympiad UKMT junior senior intermediate maths challenge smc jmc imc 2022 2023
Preparation for math olympiad UKMT junior senior intermediate maths challenge smc jmc imc 2022 2023
Preparation for math olympiad UKMT junior senior intermediate maths challenge smc jmc imc 2022 2023
The Last Question from the Senior Maths Challenge | Math Olympiad Training
Junior Kangaroo and Maths Olympiad (UKMT) preparation course (free!)
Preparation for math olympiad UKMT junior senior intermediate maths challenge smc jmc imc 2022 2023
Preparation for math olympiad UKMT junior senior intermediate maths challenge smc jmc imc 2022 2023
Preparation for math olympiad UKMT junior senior intermediate maths challenge smc jmc imc 2022 2023
Preparation for math olympiad UKMT junior senior intermediate maths challenge smc jmc imc 2022 2023
Preparation for math olympiad UKMT junior senior intermediate maths challenge smc jmc imc 2022 2023
Preparation for math olympiad UKMT junior senior intermediate maths challenge smc jmc imc 2022 2023
Preparation for math olympiad UKMT junior senior intermediate maths challenge smc jmc imc 2022 2023
Комментарии
 0:18:35
0:18:35
 0:00:51
0:00:51
 0:01:05
0:01:05
 0:03:35
0:03:35
 0:04:59
0:04:59
 0:01:31
0:01:31
 0:01:36
0:01:36
 0:08:01
0:08:01
 0:02:51
0:02:51
 0:03:21
0:03:21
 0:09:54
0:09:54
 0:04:09
0:04:09
 0:06:55
0:06:55
 0:06:54
0:06:54
 0:10:13
0:10:13
 0:02:34
0:02:34
 0:03:41
0:03:41
 0:05:07
0:05:07
 0:01:33
0:01:33
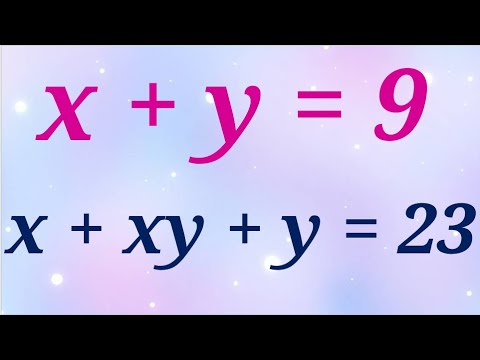 0:01:56
0:01:56
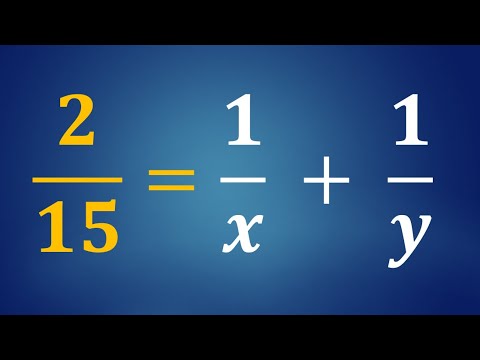 0:07:45
0:07:45
 0:10:22
0:10:22
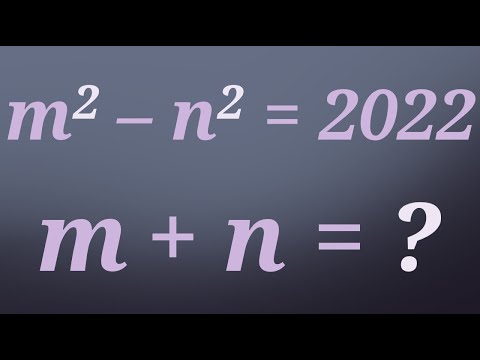 0:01:36
0:01:36
 0:03:32
0:03:32