Every Orthogonal transformation is an isometry proof | LINEAR ALGEBRA | TYBSC | MU

📐🔄 Orthogonal Transformations and Isometry: Proving the Connection
Calling all TYBSc enthusiasts at MU, set sail into the captivating realm of Linear Algebra! This session ventures deep into the intricate relationship between orthogonal transformations and isometry, exploring a detailed proof elucidating their interconnectedness.

📘 Explored Topics:
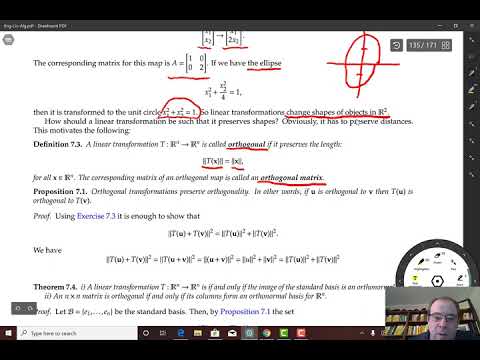
Understanding Orthogonal Transformations: Delve into transformations preserving dot products and vector lengths in the realm of vector spaces.
Deciphering Isometry: Grasp the essence of transformations that retain distances and shapes within spaces without altering their structure.
Proof Session Unveiled: Engage in an in-depth exploration unveiling the mathematical proof showcasing how every orthogonal transformation indeed serves as an isometry.
💡 Key Insights to Discover:
🧠 Grasp the pivotal role of transformations maintaining angles, lengths, and shapes within vector spaces.
📏🔍 Explore the significance of orthogonal transformations in preserving distances and shapes without alteration.
🌟 Engaging Highlights:
Step into a proof-centric session designed to unravel the inherent connection between orthogonal transformations and the principle of isometry.

▶️ Delve Into the Proof:
Embark on a mathematical journey decoding the proof that every orthogonal transformation indeed functions as an isometry here.

📢 Connect and Learn:
📚 Elevate Your Understanding:
Deepen your comprehension of Linear Algebra by unveiling the foundational linkage between orthogonal transformations and the principles of isometry!

#LinearAlgebra #OrthogonalTransformations #IsometryProof #TYBSc #MU #MathematicsEducation #ProofSessions #MathematicsAtMU

Every Orthogonal transformation is an isometry proof
For any doubts u can ask me in comment section.
If you like the video don't forget the like share and subscribe.
Thank you:) For any doubts u can ask me in comment section.
If you like the video don't forget the like share and subscribe.
Thank you:)
List Of QUIZ you can give as google form made by me:
BASIS AND DIMENSION:

Quotient Space and dimension:

Introduction to JAVA:

Characteristic Polynomial:

Property of Coset and dimension of a vector space:

Vector Space and Coset:

Please give the quiz and have more understanding of the concepts but before that please go through the concepts well.

[gopalsaw]

Sir, we can put (x-y) in the def of O.T. i.e. <T(x-y), T(x-y)>=<x-y, x-y> and the isometry follows in the next two steps.
OR
We can use the equivalent def to have,
||T(x-y)||=||(x-y)|| and again the isometry follows in next two steps.