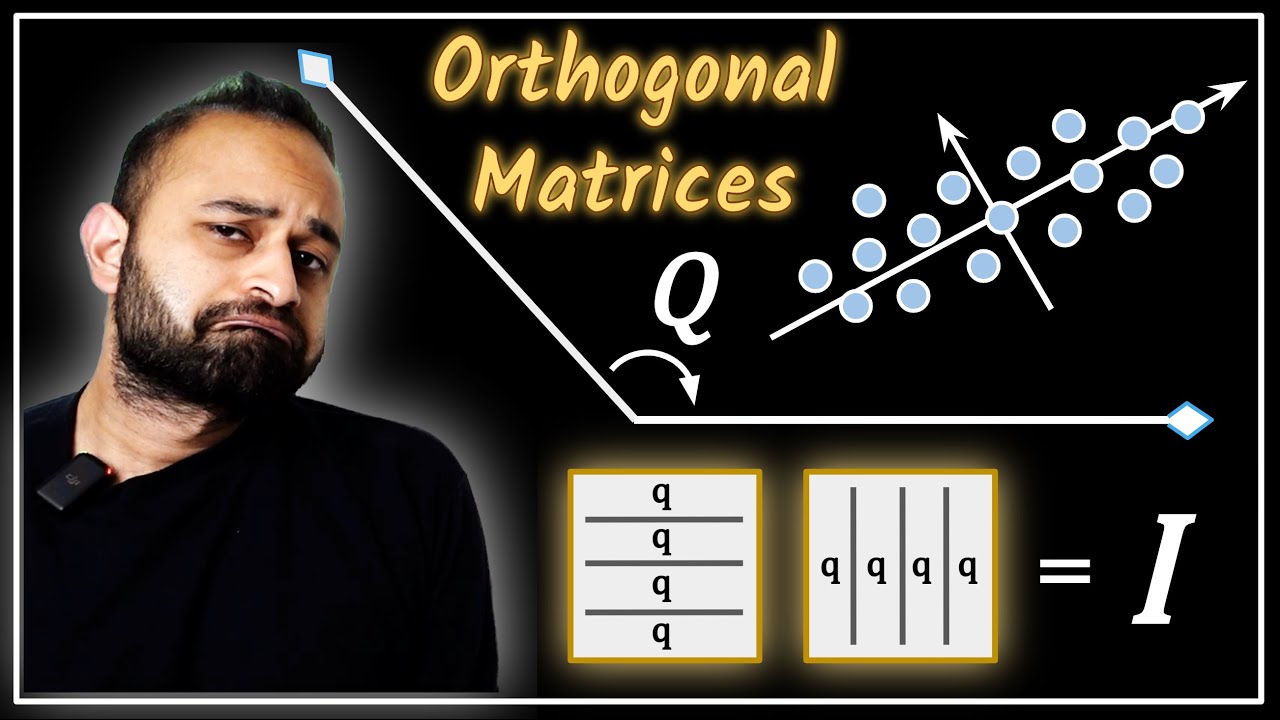
The Unexpected Power of Orthogonal Matrices

0:00 Intro
1:17 Definition
3:28 Inverse Convenience
6:31 Types of Orthogonal Transformations
10:11 Application to PCA

NOTE: I meant to say "orthogonal" instead of "linearly independent" in the verbal definition. Orthogonal means that the dot product between two vectors is 0 but linear independence means that one vector cannot be expressed as a linear combination of another vector. Thanks to some viewers for pointing this out.

[walterreuther]

This took me ages (and a lot of pain) to understand in my Multivariate Statistics class. I wish this video would have been around then... Possibly I find this video so good because I have already learned the basics, but I think this was probably the most understandable explanation of Orthogonal Matrices and PCA I have ever heard.

So... tanks! 😅

[stanislausstein]

I think you confused linear independence with orthonormality in the verbal definition.

We say that two vectors are orthogonal if their inner product is zero. Linear independence doesn't suffice for this as for example (1, 0)^T and (1, 1)^T are linearly independent, but

(1, 0) • (1, 1)^T = 1

and not 0.

I love your content btw, just wanted to point that out.

[sand]

May I request a video explaining how L1 regularization creates a sparse matrix? I have already read a few articles on the internet, but I still couldn't convince myself to fully understand the process. Your explanations on data science topics are consistently clear and concise, and I am eager to watch a video on this specific topic soon. Thank you for providing such valuable content on YouTube.

[Set_Get]

thank you for teaching/refreshing us the algebra in relatively short sessions. if possible, please include a numerical example in these videos. i love the topics you choose.

[awakerain]

Such a high-quality video! I was very uncomfortable when studying these theories without knowing the principles and finally I found this video to help me clearly figure out how these theories were worked out! Thank you so much!

[knok]

2:46 why linear independence means that dot product is zero? for example, vectors (1, 0) and (1, 1) linearly independent, but their dot product is 1*1+0*1 = 1 != 0. As I understand dot product is zero for orthogonal vectors

[ericxue]

Hi, Great video, Could you talk about the Gaussian Process in future videos? thanks very much.

[manishbhanu]

@ritvikmath Hi, can you put more insight on condition no. of orthogonal matrices n how it can deal with noise?