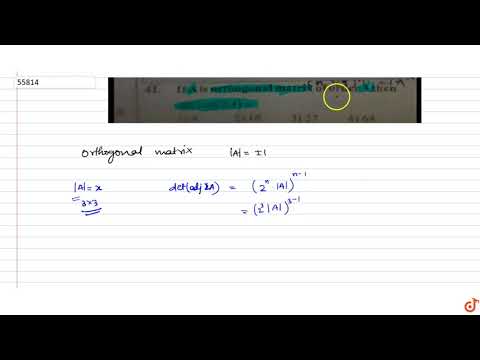
Determinant of an orthogonal matrix has value +-1

RM02

Orthogonal Matrix ( Rotation Matrix )

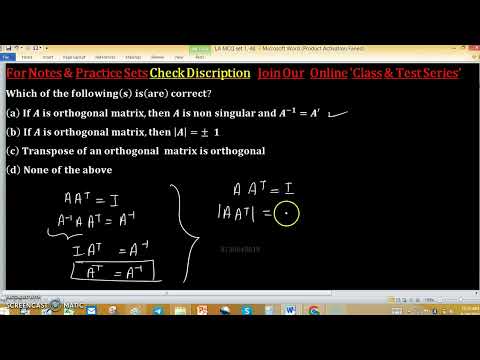
An nxn matrix is called orthogonal matrix if ATA = A AT = I

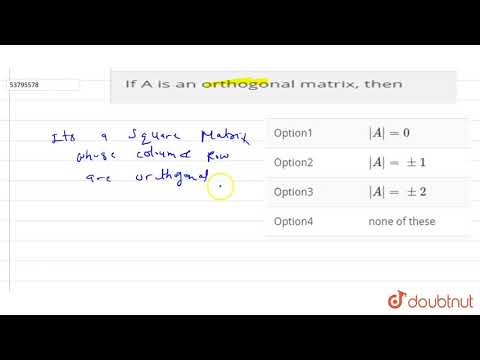
Determinant of orthogonal matrix is always +1 or –1.

Orthogonal matrix is always invertible. With its inverse = AT.

Geometrically Orthogonal matrices represent rotation ( rotational transformation ) with change in length of vector, i.e., if we premultiply a vector with orthogonal matrix then the resulting vector will be a rotated version of original vector.

The orthogonal matrix is called proper if its determinant is equal to 1.
A proper orthogonal matrix represents pure rotation.

The orthogonal matrix is called improper if its determinant is equal to –1.
An improper orthogonal matrix represents rotation with inversion ( reflection about origin ).

The columns of orthogonal matrix are orthonormal vectors.
The rows of orthogonal matrix are orthonormal vectors.

This video is uploaded by
Alpha Academy, Udaipur
Minakshi Porwal (9460189461)

[ananyamani]

Really needed is right now thank you sir

[ravikishan]

🙏Sir, show that rotation in 3-D space can be expressed by means of an orthogonal matrix wala bta digiye sir please