filmov
tv
Divergent integrals and the Cauchy principal value.
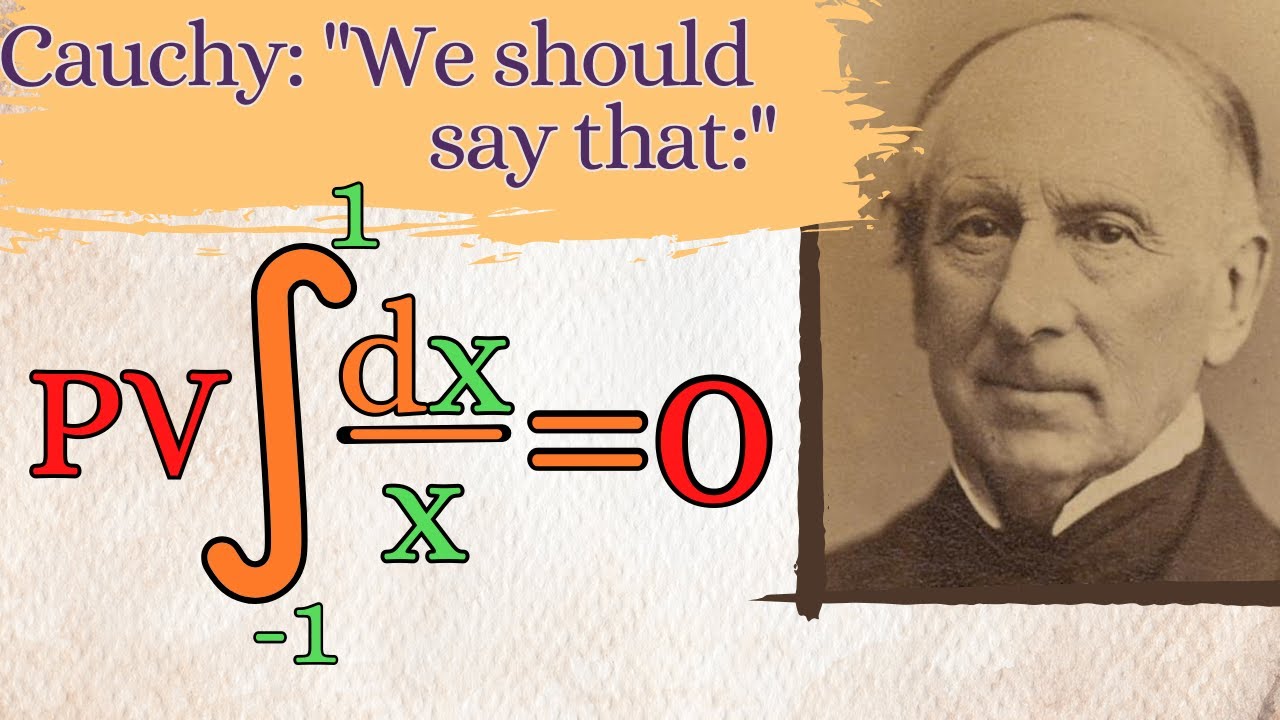
Показать описание
🌟Support the channel🌟
🌟my other channels🌟
🌟My Links🌟
🌟How I make Thumbnails🌟
🌟Suggest a problem🌟
🌟my other channels🌟
🌟My Links🌟
🌟How I make Thumbnails🌟
🌟Suggest a problem🌟
Divergent integrals and the Cauchy principal value.
Cauchy Principal Value Integral (simplified concept & examples)
Integral Test | Derivation & 1st Example
How REAL Men Integrate Functions
Comparison test for convergence and divergence of improper integrals
Definite integral 1/(x-1): divergence vs. Cauchy Principal Value. Integral with vertical asymptote.
Evaluating Real Integrals Part 2 | Improper Integrals | Complex Analysis #19
improper integral of x from neg inf to inf
Complex integration, Cauchy and residue theorems | Essence of Complex Analysis #6
Calculus 2 - Integral Test For Convergence and Divergence of Series
Cauchy Convergence criteria for improper integral of second and third kind || Improper Integral
Cauchy Principal Value
Art. 2.13.1 Cauchy's Test for Improper Integral at infinity
what's the integral of 1/x from -1 to 1
Calculus 2 Lecture 9.1: Convergence and Divergence of Sequences
Lec-14_nth Term Test for Divergence & Cauchy Integral Test | Mathematics 1 | First Year Engineer...
Infinite Series - Cauchy's Integral Test For Convergence of Series
Lec-32_nth-Term Test for Divergence, Cauchy's Integral Test | Mathematics-1 | First Year Engine...
Cauchy's Integral Test | Numericals | Infinite Series | Convergence & Divergence | Maths 1 ...
Proof of Cauchy Integral Test
Convergence and divergence of series_ Cauchy's integral test_ part 10
Real Analysis 64 | Cauchy Principal Value
Convergence and Divergence - Introduction to Series
Cauchy Integral test for convergence | Infinite series | convergent divergent series | Examples
Комментарии
 0:13:50
0:13:50
 0:14:04
0:14:04
 0:08:55
0:08:55
 0:00:35
0:00:35
 0:16:56
0:16:56
 0:07:05
0:07:05
 0:17:01
0:17:01
 0:08:54
0:08:54
 0:40:45
0:40:45
 0:28:17
0:28:17
 0:17:54
0:17:54
 0:12:22
0:12:22
 0:03:38
0:03:38
 0:04:01
0:04:01
 2:27:29
2:27:29
 0:15:30
0:15:30
 0:13:20
0:13:20
 0:15:00
0:15:00
 0:17:51
0:17:51
 0:15:08
0:15:08
 0:32:56
0:32:56
 0:09:16
0:09:16
 0:16:18
0:16:18
 0:14:01
0:14:01