filmov
tv
Cauchy Principal Value
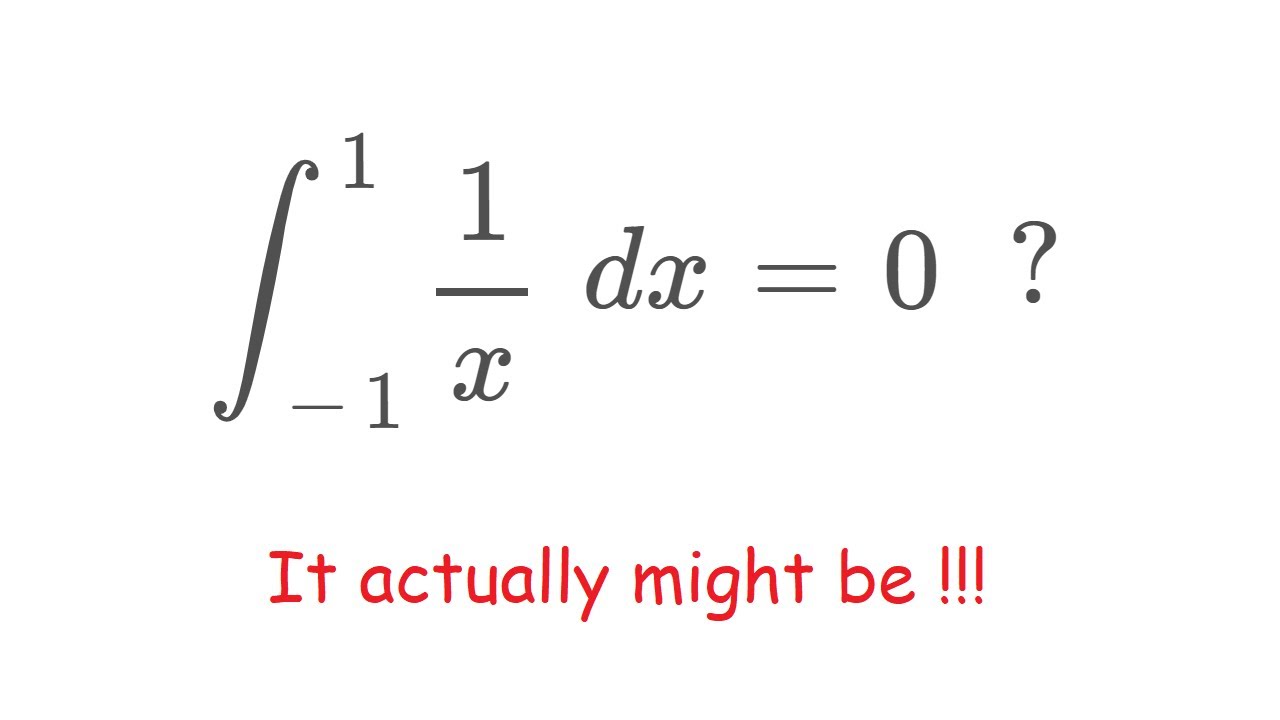
Показать описание
Cauchy principal value integral example. You learn in calculus courses that an improper integral is sometimes divergent, but in this video I show you how to make it (rigorously) equal to zero! This is widely used in distribution theory and Fourier analysis
Divergent integrals and the Cauchy principal value.
Cauchy Principal Value
Cauchy Principal Value Integral (simplified concept & examples)
[CA/Week 3] 12. Principal value integration
Cauchy principal value
Computing Improper Integrals using the Residue Theorem | Cauchy Principal Value
4. Improper Integrals | Cauchy Principle Value
Lecture 07: Cauchy Principle Value
Lecture 03 : Cauchy Principal value theorem
cauchy principal value
Cauchy Principal Value Example Part 1
Cauchy Principle Value and Indented Paths
Definite integral 1/(x-1): divergence vs. Cauchy Principal Value. Integral with vertical asymptote.
Cauchy Principal Part
cauchy principal value and general value | improper integrals bsc 1st year
GATE MA 2009 || Complex Analysis Solution || Cauchy Principal Value of Integral ||
improper integral cauchy principal value and general value question for bsc
what's the integral of 1/x from -1 to 1
Improper integrals and the principal value
Cauchy Principal Value. Presented by pratiksha kale , ujjwal chamate ,MSc sem l
Cauchy principal value | Wikipedia audio article
Calculate an Improper Integral 2/x
cauchy principal value
Cauchy Principal Value & Counting poles and zeros: Mathematical Physics III #9.1 | ZC OCW
Комментарии
 0:13:50
0:13:50
 0:12:22
0:12:22
 0:14:04
0:14:04
![[CA/Week 3] 12.](https://i.ytimg.com/vi/upfh13N9SOc/hqdefault.jpg) 0:06:00
0:06:00
 0:06:21
0:06:21
 0:13:41
0:13:41
 0:10:12
0:10:12
 1:00:42
1:00:42
 0:21:51
0:21:51
 0:13:41
0:13:41
 0:07:29
0:07:29
 0:22:47
0:22:47
 0:07:05
0:07:05
 0:40:40
0:40:40
 0:02:25
0:02:25
 0:16:19
0:16:19
 0:03:41
0:03:41
 0:04:01
0:04:01
 0:07:01
0:07:01
 0:03:26
0:03:26
 0:26:24
0:26:24
 0:06:58
0:06:58
 0:15:24
0:15:24
 1:08:15
1:08:15