filmov
tv
Given the measure of one interior angle find the number of sides for a polygon

Показать описание
👉 Learn how to determine the number of sides of a regular polygon. A polygon is a plane shape bounded by a finite chain of straight lines. A regular polygon is a polygon whose sides are congruent (equal). The interior angle of a polygon is the angle between two sides of the polygon. For a regular polygon, the interior angles are congruent (equal).
The sum of the interior angles of a regular polygon is given by the formula: 180(n - 2) degrees, where n is the number of sides of the polygon. Thus, given one of the interior angles of a polygon, say m, to find the number of sides of the polygon, we solve for n in the equation: 180(n - 2) = mn, where m is the given interior angle measure.
Organized Videos:
✅Polygons
✅Sum of Exterior Angles of a Polygon
✅One Exterior Angle of a Polygon
✅Number of Sides of a Regular Polygon
✅Sum of Interior Angles of a Polygon
✅One Interior Angle of a Polygon
✅Interior Angle Sum of a Polygon
✅Interior and Exterior Angles of Polygons
✅Classify Polygons
✅Congruent Polygons
✅Similar Polygons
Connect with me:
#Polygons #brianmclogan
The sum of the interior angles of a regular polygon is given by the formula: 180(n - 2) degrees, where n is the number of sides of the polygon. Thus, given one of the interior angles of a polygon, say m, to find the number of sides of the polygon, we solve for n in the equation: 180(n - 2) = mn, where m is the given interior angle measure.
Organized Videos:
✅Polygons
✅Sum of Exterior Angles of a Polygon
✅One Exterior Angle of a Polygon
✅Number of Sides of a Regular Polygon
✅Sum of Interior Angles of a Polygon
✅One Interior Angle of a Polygon
✅Interior Angle Sum of a Polygon
✅Interior and Exterior Angles of Polygons
✅Classify Polygons
✅Congruent Polygons
✅Similar Polygons
Connect with me:
#Polygons #brianmclogan
Find the number of sides of a regular polygon, given the measure of one interior ang
Given the measure of one interior angle find the number of sides for a polygon
How to find the measure of one exterior angle given number of sides for a regular polygon
Determine the measure of one interior angle given the sum of interior angles ex 3
How to find the measure of one exterior angle given the number of sides ex 1
How to find the measure of one exterior angle of a regular polygon
Given one interior angle, find the number of sides of the regular polygon
Given one exterior angle, learn how to find the number of sides of a polygon ex 2
What is the formula to find the measure of one interior angle
How to determine the number of sides of a regular polygon, given one interior angle
How to draw a triangle, given the length of two sides and the measures of one angle (Step by Step)
Finding the measure of One Exterior Angle of a Regular Polygon | Matatag Curriculum | Grade 7 |
The measure of one angle of a parallelogram is 70°. What are the measures of the remaining angles?
How to determine the measure of one exterior angle given the number of sides ex 3
How To Calculate The Interior Angles and Exterior Angles of a Regular Polygon
How do you find the measure of one interior angle of a polygon
How to determine the number of sides given one interior angle
Finding the measure of One Interior Angle of a Regular Polygon | Matatag Curriculum | Grade 7 |
How to draw a triangle, given the length of one side and the measures of two angles (Step by Step)
Learn to find the number of sides of a regular polygon when given one exterior angle
Finding the Measure of Angles in a Polygon | Matatag Curriculum | Grade 7 | Explain in Detailed |
Exterior Angle Theorem: How to find the measure of Angles?
Using Parallel Lines to Find the Measure of Angles
How to find the measure of an individual angle when given the sum of interior angles
Комментарии
 0:02:38
0:02:38
 0:03:05
0:03:05
 0:02:39
0:02:39
 0:02:54
0:02:54
 0:02:52
0:02:52
 0:04:41
0:04:41
 0:02:26
0:02:26
 0:03:02
0:03:02
 0:01:38
0:01:38
 0:04:12
0:04:12
 0:02:00
0:02:00
 0:05:57
0:05:57
 0:03:25
0:03:25
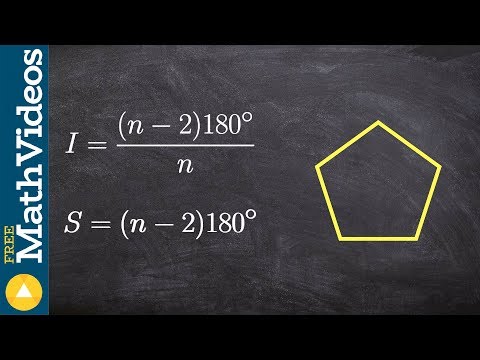 0:02:55
0:02:55
 0:13:13
0:13:13
 0:03:24
0:03:24
 0:05:05
0:05:05
 0:08:38
0:08:38
 0:02:29
0:02:29
 0:01:16
0:01:16
 0:24:47
0:24:47
 0:03:36
0:03:36
 0:02:00
0:02:00
 0:02:03
0:02:03