Using Parallel Lines to Find the Measure of Angles

👉 Learn how to solve for an unknown variable using parallel lines and a transversal theorems. Two lines are said to be parallel when they have the same slope and are drawn straight to each other such that they cannot meet. In geometry, parallel lines are identified by two arrow heads or two small lines indicated in both lines.

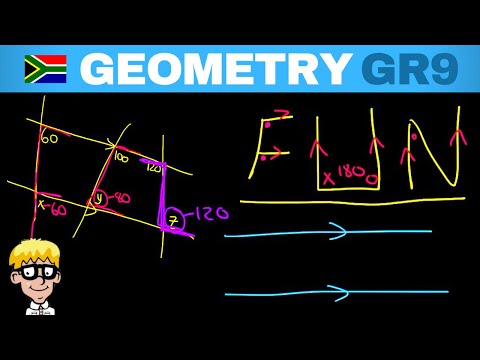
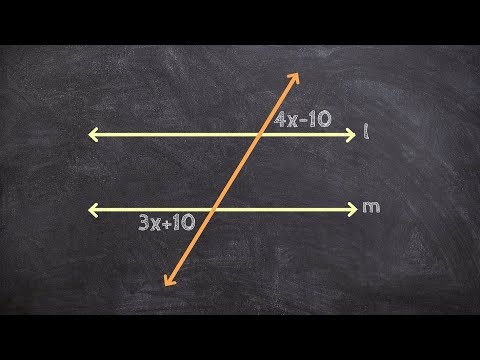
A transversal is a straight line crossing two parallel lines. There are various angle relationships formed when a transversal crosses two parallel lines. They include: alternate interior angles, alternate exterior angles, corresponding angles, consecutive interior angles, etc.

The theorems of the angle relationships include: alternate interior angles are equal, alternate exterior angles are equal, consecutive interior angles are supplementary (equal to 180 degrees), corresponding angles are equal.

Given expressions representing the angles formed by two parallel lines and a transversal, we can make use of the parallel line/ transversal angle relationships and usual angle properties to solve for the unknown variable in the expressions.

Organized Videos:
✅Parallel Lines and a Transversal
✅Parallel Lines and a Transversal Converse Theorems
✅Parallel Lines and a Transversal Theorems
✅Label Angles formed by Parallel Lines and a Transversal
✅Define Angles formed by Parallel Lines and a Transversal
✅Parallel Lines cut by a Transversal Solve for x
✅Find the value x that proves two lines are parallel
✅Parallel Lines and a Transversal | Proofs
✅Algebraic Proofs

Connect with me:

#parallellinesandatransversal #brianmclogan

[VroskiVA]

I know this video was made in 2013, but this teacher clearly knows what he's doing. Currently stuck in quarantine and zoom calls aint doing NOTHING to my brain.
Seriously helped me get a passing mark on my grades!

[me.]

I admit i didnt pay attention in class, and now im looking for videos that could help me- 🤦‍♀️

[nadiagerard]

Thank you so much! Had a hard time grasping this in class but you've explained it perfectly!

[lizbethvillanuevaandwonder]

Everything but what I’m looking for is not on here

[vr]

you always come in clutch when my teachers over complicate things. I passed my exams because of you, thank you

[runningcloud]

This man just saved me from failing a test. THANK YOU!!!!

[Renjitookmyheart]

..my dumb ass didn’t pay attention during virtual....

[smackedpreschooler]

currently have a 55 in math, hope this helps me, it comes across simply

[cubi_]

This actually helped me a lot, thank you!

[Mxgchef]

This is my first time acknowledging the math subject

[kitumessi]

This is esthetic interest.for those who essential are interest in maths. And it's interest and understandable I like it

[Hustonian]

I kinda feel like he is talking to himself. but if not its cool that he was recording his class back in 2013

[Numberonedjofanever]

This guy's been teaching me math since I was like 12

[renejperez]

Your the best everything that you show help me ! Thanks

[OrangeBulbs]

Math is all fun and games until you add shapes into it

[esydeleted]

geometry is the sole reason i want to drop out.

[gabeitch-]

POV your watching this while writing your math exam

[shubhangimhatre]

Toughest subject in the world....maths

[pfiucrt]

Guess who didn't focus in online class

[nic_hon]

can you be my teacher please i will PAY you!