Rotating dynamical billiards

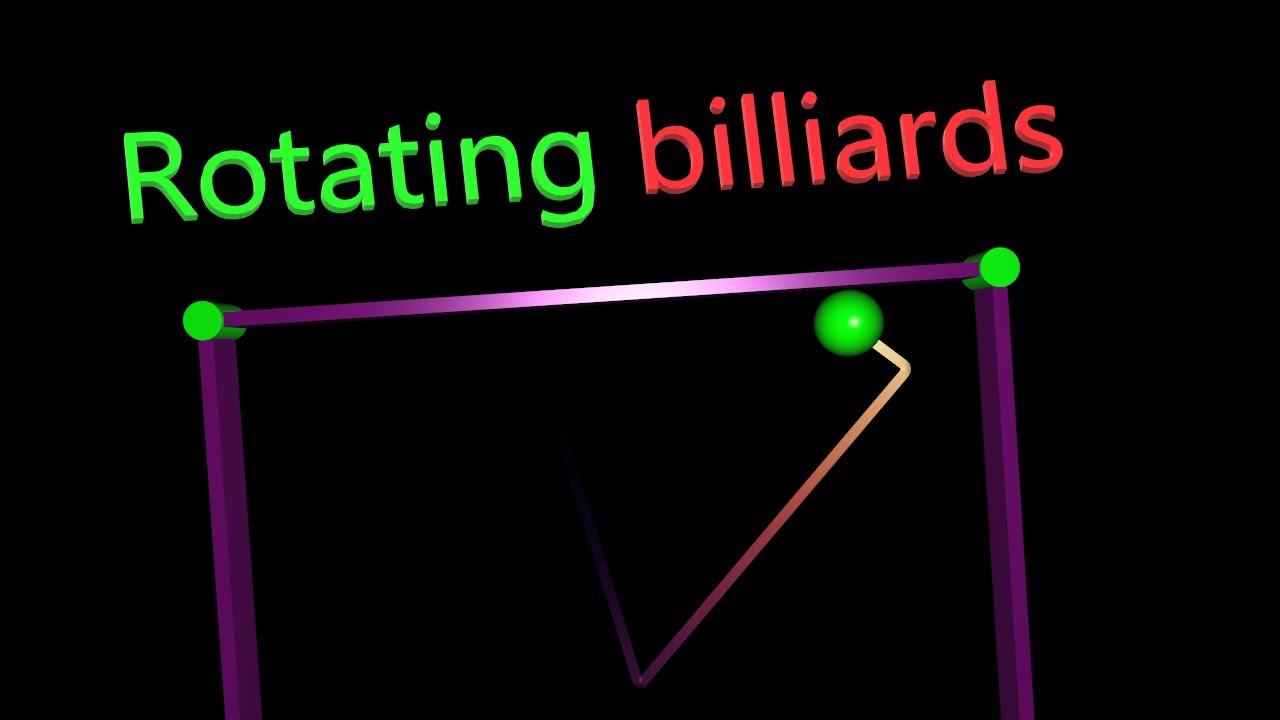
Simulation of rotating dynamical billiards. The particle is regarded as a soft sphere as its interaction with the boundaries is defined by a smooth and compactly supported potential. The boundaries are physical and have the same combined mass as the sphere.

Simulation are performed for square and triangular billiards. The billiards are presented in the inertial frame of reference and in the billiard rotating frame of reference. The sphere position is tracked on the canvas to display the long term dynamical behavior.

0:00 rectangular, rotating frame, regular
0:38 rectangular, inertial frame, regular
1:09 rectangular, both, regular
1:16 rectangular, both, regular
1:24 rectangular, both, chaotic
1:46 triangular, both, chaotic
1:55 triangular, both, regular
2:02 triangular, both, regular
2:09 triangular, both, regular

The dynamical system is treated as a Hamiltonian system with two degrees of freedom and with the billiard rotation regarded as a cyclic coordinate.

The simulations were performed using high order explicit symplectic integrators and were rendered in real time.

🎵 "3D Galax" remix by Dubmood. Original from "3D Galax" title theme composed by Ben Daglish.

[PendragonDaGreat]

I'm a little confused as to why some of the paths are curved. Is that the rotating frame of reference at work? If so what exactly is rotating?