filmov
tv
Calculating the Surface Area of an Object with Integration in Calculus

Показать описание
Welcome to our fascinating YouTube video on calculating the surface area of objects using calculus! In this enlightening tutorial, we delve into the realm of calculus and showcase how integration can be a powerful tool for determining the surface area of various complex objects.
Whether you're a student navigating the intricacies of calculus or an enthusiast seeking a deeper understanding of surface area calculations, this video is your gateway to unlocking the potential of calculus in determining surface areas. Our expert instructor breaks down complex concepts into digestible explanations, ensuring that you grasp the essence of calculus-based surface area calculations.
Join us as we embark on a mathematical journey, exploring the principles of integration and their applications in calculating surface areas. We demonstrate how integration can be used to break down complex surfaces into infinitesimally small elements, allowing us to sum up their individual contributions to obtain the total surface area.
Through step-by-step examples and interactive visuals, we tackle a variety of objects, including curved surfaces, solids of revolution, and more. We explore the concept of parametric equations and how they can be employed to compute the surface area of intricate shapes.
With our comprehensive explanations and insightful demonstrations, you'll develop a solid foundation in using calculus to calculate surface areas. You'll gain a deep appreciation for the elegance and versatility of integration as a mathematical tool.
Don't let the complexities of surface area calculations deter you any longer. Join us for this illuminating tutorial and unlock the power to confidently determine surface areas using calculus. Hit that play button now and embark on your journey to becoming a master of surface area calculations!
Whether you're a student navigating the intricacies of calculus or an enthusiast seeking a deeper understanding of surface area calculations, this video is your gateway to unlocking the potential of calculus in determining surface areas. Our expert instructor breaks down complex concepts into digestible explanations, ensuring that you grasp the essence of calculus-based surface area calculations.
Join us as we embark on a mathematical journey, exploring the principles of integration and their applications in calculating surface areas. We demonstrate how integration can be used to break down complex surfaces into infinitesimally small elements, allowing us to sum up their individual contributions to obtain the total surface area.
Through step-by-step examples and interactive visuals, we tackle a variety of objects, including curved surfaces, solids of revolution, and more. We explore the concept of parametric equations and how they can be employed to compute the surface area of intricate shapes.
With our comprehensive explanations and insightful demonstrations, you'll develop a solid foundation in using calculus to calculate surface areas. You'll gain a deep appreciation for the elegance and versatility of integration as a mathematical tool.
Don't let the complexities of surface area calculations deter you any longer. Join us for this illuminating tutorial and unlock the power to confidently determine surface areas using calculus. Hit that play button now and embark on your journey to becoming a master of surface area calculations!
Комментарии
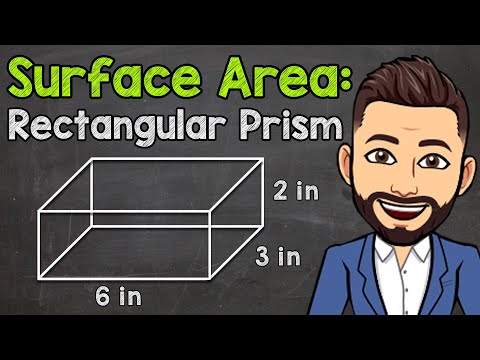 0:04:57
0:04:57
 0:05:35
0:05:35
 0:06:42
0:06:42
 0:11:14
0:11:14
 0:01:06
0:01:06
 0:03:33
0:03:33
 0:06:49
0:06:49
 0:16:51
0:16:51
 0:32:11
0:32:11
 0:04:06
0:04:06
 0:30:36
0:30:36
 0:01:42
0:01:42
 0:05:14
0:05:14
 0:09:26
0:09:26
 0:04:59
0:04:59
 0:08:42
0:08:42
 0:16:23
0:16:23
 0:02:53
0:02:53
 0:05:39
0:05:39
 0:10:26
0:10:26
 0:02:45
0:02:45
 0:08:20
0:08:20
 0:24:23
0:24:23
 0:02:24
0:02:24