filmov
tv
Rotation Matrix, Euler Angles, Principal Axis-Angle of Rotation, 3D Rigid Body Kinematics Lecture 12

Показать описание
Dr. Shane Ross, Virginia Tech Engineering. Lecture 12 of a course on analytical dynamics (Newton-Euler, Lagrangian dynamics, and 3D rigid body dynamics). To describe the orientation (that is, attitude) of a 3D rigid body, we describe the orientation of the frame attached to the body, that is, the triad of unit vectors that define the B-frame. We seek to describe the triad of unit vectors that define the B-frame with respect to the triad of unit vectors that define the inertial I-frame. This is commonly done using a rotation matrix, C, the direction cosine matrix.
► Next: Rigid body kinematic differential equation for Euler angles and rotation matrix
► Previous, Rotational dynamics about an arbitrary reference point, planar rigid body motion, car jump example
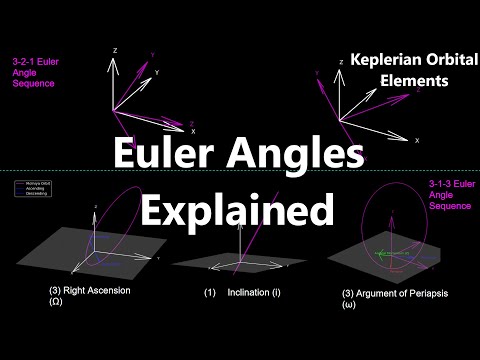
We gently introduce this using a 2D version, rotation about a single matrix, where only one angle is necessary to parameterize the 2 x 2 rotation matrix. Then we consider the rotation matrix for 3D frames. A common way to parameterize the 3 x 3 rotation matrix is via Euler angles, which involves writing the arbitrary 3 x 3 rotation matrix in terms of a product of three rotation matrices about axes. We describe the twelve Euler angle conventions and go through the 3-2-3 example in detail.
According to Euler's theorem, any arbitrary rotation can be described as a rotation through some angle about some axis, called the principal axis. We introduce these notions as well, including the Rodrigues' rotation formula for writing the rotation matrix C in terms of the principal axis and angle.
CORRECTION: There's an error in the formula for the principal angle phi near the end of the lecture. The correct formula is:
phi = arccos ( 0.5*( trace(C) - 1) )
►Dr. Shane Ross, Virginia Tech aerospace professor (Caltech PhD)
► Follow me on Twitter
► The entire playlist of 29 videos for this course:
► Textbook used:
Engineering Dynamics: A Comprehensive Introduction
by N. Jeremy Kasdin and Derek A. Paley
Lecture 2020-10-01, Fall 2020
Author's website:
► Courses and Playlists by Dr. Ross
📚Attitude Dynamics and Control
📚Nonlinear Dynamics and Chaos
📚Hamiltonian Dynamics
📚Three-Body Problem Orbital Mechanics
📚Lagrangian and 3D Rigid Body Dynamics
📚Center Manifolds, Normal Forms, and Bifurcations
#RigidBody #EulerAngles #attitudeDynamics #orientation #BryanTait #TaitBryan #rotation #matrix #EulersTheorem #EulerAxis #PrincipalAxis #PrincipalRotationVector
► Next: Rigid body kinematic differential equation for Euler angles and rotation matrix
► Previous, Rotational dynamics about an arbitrary reference point, planar rigid body motion, car jump example
We gently introduce this using a 2D version, rotation about a single matrix, where only one angle is necessary to parameterize the 2 x 2 rotation matrix. Then we consider the rotation matrix for 3D frames. A common way to parameterize the 3 x 3 rotation matrix is via Euler angles, which involves writing the arbitrary 3 x 3 rotation matrix in terms of a product of three rotation matrices about axes. We describe the twelve Euler angle conventions and go through the 3-2-3 example in detail.
According to Euler's theorem, any arbitrary rotation can be described as a rotation through some angle about some axis, called the principal axis. We introduce these notions as well, including the Rodrigues' rotation formula for writing the rotation matrix C in terms of the principal axis and angle.
CORRECTION: There's an error in the formula for the principal angle phi near the end of the lecture. The correct formula is:
phi = arccos ( 0.5*( trace(C) - 1) )
►Dr. Shane Ross, Virginia Tech aerospace professor (Caltech PhD)
► Follow me on Twitter
► The entire playlist of 29 videos for this course:
► Textbook used:
Engineering Dynamics: A Comprehensive Introduction
by N. Jeremy Kasdin and Derek A. Paley
Lecture 2020-10-01, Fall 2020
Author's website:
► Courses and Playlists by Dr. Ross
📚Attitude Dynamics and Control
📚Nonlinear Dynamics and Chaos
📚Hamiltonian Dynamics
📚Three-Body Problem Orbital Mechanics
📚Lagrangian and 3D Rigid Body Dynamics
📚Center Manifolds, Normal Forms, and Bifurcations
#RigidBody #EulerAngles #attitudeDynamics #orientation #BryanTait #TaitBryan #rotation #matrix #EulersTheorem #EulerAxis #PrincipalAxis #PrincipalRotationVector
Комментарии
 1:06:01
1:06:01
 0:00:32
0:00:32
 0:04:41
0:04:41
 0:11:14
0:11:14
 0:00:21
0:00:21
 0:07:50
0:07:50
 0:05:59
0:05:59
 0:01:00
0:01:00
 1:12:05
1:12:05
 0:09:20
0:09:20
 0:07:07
0:07:07
 0:05:05
0:05:05
 0:57:21
0:57:21
 0:05:09
0:05:09
 0:17:00
0:17:00
 0:19:34
0:19:34
 0:17:38
0:17:38
 0:10:40
0:10:40
 0:08:25
0:08:25
 0:11:24
0:11:24
 0:00:44
0:00:44
 0:13:23
0:13:23
 0:08:19
0:08:19
 0:16:33
0:16:33