filmov
tv
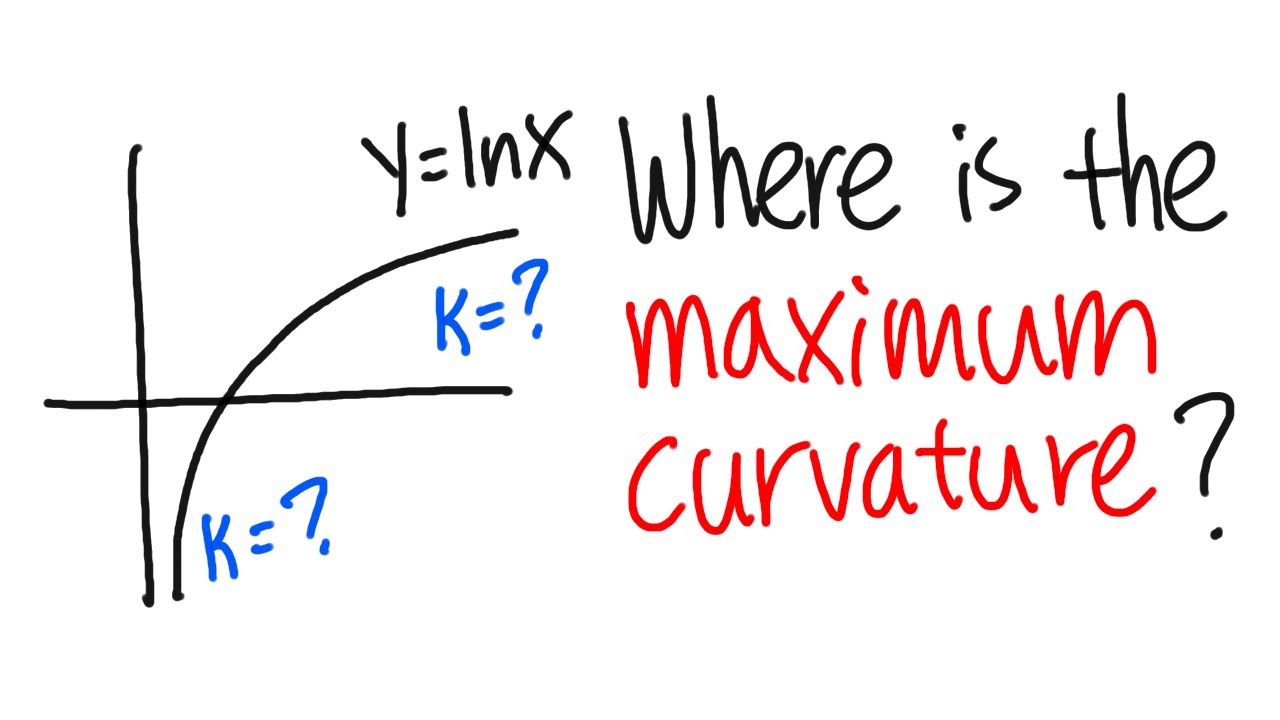
At what point does y=ln(x) have the maximum curvature?
Показать описание
-----------------------------
Support this channel and get my calculus notes on Patreon: 👉
-----------------------------
#calculus #bprpcalculus #apcalculus #tutorial #math
Support this channel and get my calculus notes on Patreon: 👉
-----------------------------
#calculus #bprpcalculus #apcalculus #tutorial #math
At what point does y=ln(x) have the maximum curvature?
Graphing the Natural Log Function y = ln x
how do we know the derivative of ln(x) is 1/x (the definition & implicit differentiation)
What is e and ln(x)? (Euler's Number and The Natural Logarithm)
Derivative of y = ln x (Natural Log)
Natural Logarithms
y=lnx and y=kx are tangent
How to differentiate natural logarithm y=ln(x) by considering x=e^y & finding dx/dy
IIT Alumni Reveal Their Secret GATE Math Strategy
What does LN(x) = in math?
Take the derivative of the natural log function
Graphing y=ln x
2nd derivative of y=ln(x+y)
Find the derivative of y = (ln x)^4
How to differentiate (ln x)/x
Graph of Natural Logarithm y = ln(x)
Introduction to Logarithmic Differentiation
10Q Quick! Graph y = ln(x)
Derivative of y = (ln x)^3
Differentiate y=ln(x^3)
How to Differentiate y=ln(lnx) using the Chain Rule
Find the derivative of y = ln(ln x). General logarithmic exponential functions
Graph y=ln(x+1)
Find the equation of the line normal of y=ln(x+4) at (-3, 0).
Комментарии
 0:10:27
0:10:27
 0:05:18
0:05:18
 0:16:49
0:16:49
 0:12:02
0:12:02
 0:04:00
0:04:00
 0:02:49
0:02:49
 0:05:19
0:05:19
 0:00:58
0:00:58
 0:52:43
0:52:43
 0:12:03
0:12:03
 0:00:43
0:00:43
 0:02:49
0:02:49
 0:05:38
0:05:38
 0:00:40
0:00:40
 0:01:53
0:01:53
 0:08:36
0:08:36
 0:13:31
0:13:31
 0:02:04
0:02:04
 0:00:44
0:00:44
 0:02:06
0:02:06
 0:01:33
0:01:33
 0:02:36
0:02:36
 0:02:33
0:02:33
 0:02:19
0:02:19