filmov
tv
Integral of sin^5(x)

Показать описание
Integral of sin^5(x),
integral of sin^5 x
integral of (sin(x))^5
trig integrals, trigonometric integrals, integral of sin(x), integral of tan(x), integral of sec(x), James Stewart single variable Calculus sect 7.2, integration examples, integral examples, antiderivative examples, u substitution examples, integral practice problems, calculus 2 practice problems, blackpenredpen,
algebra, solving equations, solving inequality, pierce college, algebra solution, algebra exam, order of operations, fractions, factoring, calculus, exponents, learn algebra, math 115 pierce college, math 125 pierce college, ASAP pierce college, Steve Chow, blackpenredpen, whitechalkredchalk
integral of sin^5 x
integral of (sin(x))^5
trig integrals, trigonometric integrals, integral of sin(x), integral of tan(x), integral of sec(x), James Stewart single variable Calculus sect 7.2, integration examples, integral examples, antiderivative examples, u substitution examples, integral practice problems, calculus 2 practice problems, blackpenredpen,
algebra, solving equations, solving inequality, pierce college, algebra solution, algebra exam, order of operations, fractions, factoring, calculus, exponents, learn algebra, math 115 pierce college, math 125 pierce college, ASAP pierce college, Steve Chow, blackpenredpen, whitechalkredchalk
Integral of sin^5(x)
Integral of sin^5(x)
Integral of sin 5x
Integral of sin^5x ❖ Calculus ❖ Trig Integrals
integration of sin^5(x) between 0 and pi/2
|| Evaluate integral sin^5.x.cis^3.x .dx || in Telugu || engineering mathematics 2 || diploma ||
Find the integral of sin^5x using the power reduction formula
Evaluate the Integral from 0 to pi/2 sin^5 x dx with U Substitution. Example 4
Calculus 2 Exam Review Part6
integrate sin(5/x)/x^2 dx
Trigonometric Integrals the Integral of sin(5x)*cos(4x)
Integral of (sin^5x)(cos^2x) ❖ Calculus 2 ❖ Trig Integrals
Integrating ( sin x ) ^ 5 Using a Reduction Formula
Integral of sin(x)/cos^5(x) (substitution)
Integral of sin^5(x)*cos(x) - Integral example
The Integral of sin(5x)*cos(4x) Can Be Done in Many Ways
Integrate (sinx)^5 (cosx)^3 by u-substitution
The value of the definite integral, `int_0^(pi/2) (sin5x)/sinx dx` is
Integral of Sin^5(x)
Evaluate the Definite Integral from 0 to 2pi of sin^7 x cos^5 x dx with U Substitution.
Trigonometric Integrals
THE INTEGRAL OF SIN^5 3X.
Integral of sin(5x)*sin(3x)
Evaluate the integral. sin^(7)x cos^(5)x dx
Комментарии
 0:04:38
0:04:38
 0:03:56
0:03:56
 0:02:32
0:02:32
 0:05:11
0:05:11
 0:07:29
0:07:29
 0:04:50
0:04:50
 0:05:32
0:05:32
 0:04:21
0:04:21
 5:47:36
5:47:36
 0:01:24
0:01:24
 0:02:28
0:02:28
 0:06:00
0:06:00
 0:05:25
0:05:25
 0:01:37
0:01:37
 0:01:45
0:01:45
 0:09:22
0:09:22
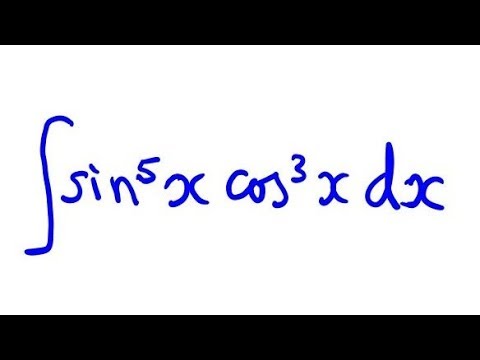 0:04:21
0:04:21
 0:04:58
0:04:58
 0:04:01
0:04:01
 0:04:46
0:04:46
 0:31:29
0:31:29
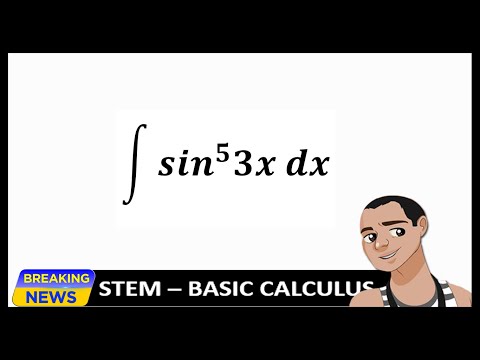 0:05:47
0:05:47
 0:02:05
0:02:05
 0:08:14
0:08:14