filmov
tv
Evaluate the integral. sin^(7)x cos^(5)x dx
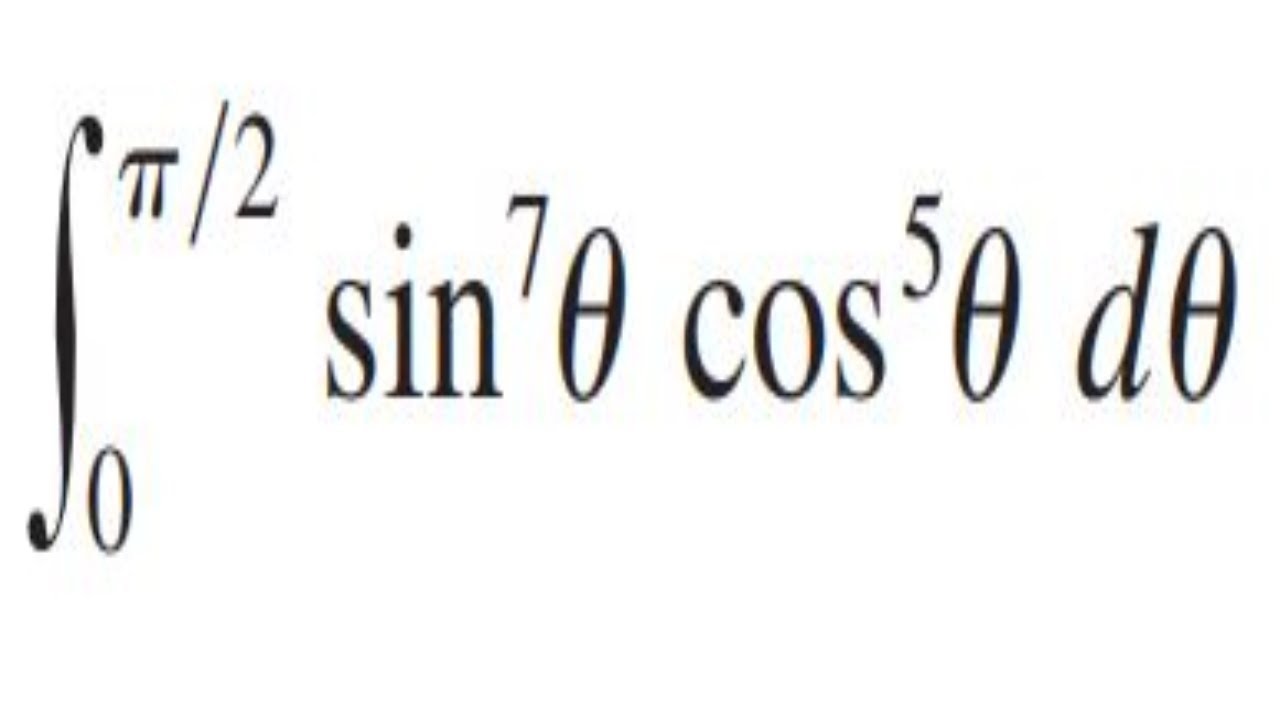
Показать описание
Evaluate the integral. sin^(7)x cos^(5)x dx .
Evaluate the integral. sin^(7)x cos^(5)x dx
Evaluate the Definite Integral from 0 to 2pi of sin^7 x cos^5 x dx with U Substitution.
#shorts: int(sin^7(x)cos^5(x))dx
integral of sin^7(x)*cos(x) dx
int sen^7 x cos^5 x dx
Integral of sin^7(x) dx (ILIEKMATHPHYSICS)
Integral of sin^7 x cos x
integrate sin(7x) dx
Revision for MAT2054
Evaluate the integral from 0 to 𝜋/2 of [(sin^7(𝜃))(cos^5(𝜃))] d𝜃
Trigonometric Integrals
Integral of sin(8x)cos(5x), calculus 2 tutorial
THE INTEGRAL OF SIN3X COS5X
The value of integral ∫_0^(π/2)〖sin^3x cos^(5/2)x dx〗 is:(a) 8/77 (b) 4/77 (c) 4/7 (d) 8/7...
Class 12th – Integral of Sin^2 x Cos^7 x dx | Integrals | Tutorials Point
Trigonometric Integrals the Integral of sin(5x)*cos(4x)
Sin^7x integration
Integral of sin 7x sin 3x || Integration of trigonometric functions
Using the Beta and Gamma functions to resolve an interesting trig integral
Integral of sin^3(x)cos^5(x) - Integral example
`int(cos7x-cos8x)/(1+2cos 5x)dx=`
Integrals#9 ~ Integral of [(sin 7x)(sin 9x)] dx
Integral of cos(x)sin^7(x) - Integral example
`int_0^pi xsin^7x cos^6xdx`
Комментарии
 0:08:14
0:08:14
 0:04:46
0:04:46
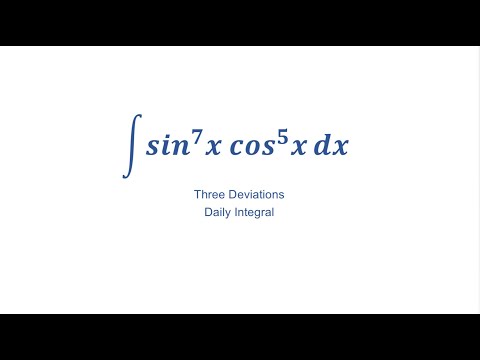 0:00:40
0:00:40
 0:02:11
0:02:11
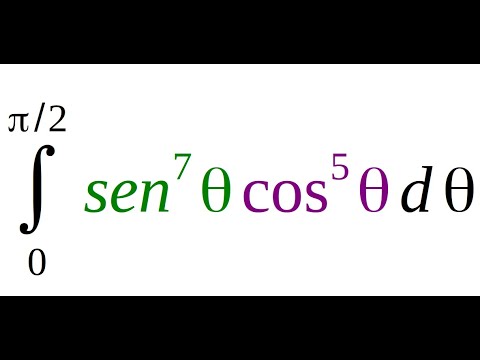 0:06:52
0:06:52
 0:02:38
0:02:38
 0:02:42
0:02:42
 0:00:56
0:00:56
 0:46:48
0:46:48
 0:04:04
0:04:04
 0:31:29
0:31:29
 0:02:50
0:02:50
 0:04:00
0:04:00
 0:03:28
0:03:28
 0:05:51
0:05:51
 0:02:28
0:02:28
 0:02:54
0:02:54
 0:02:29
0:02:29
 0:08:04
0:08:04
 0:02:32
0:02:32
 0:05:49
0:05:49
 0:01:09
0:01:09
 0:02:14
0:02:14
 0:05:51
0:05:51