filmov
tv
How to Solve Cubic Equations with Complex Roots
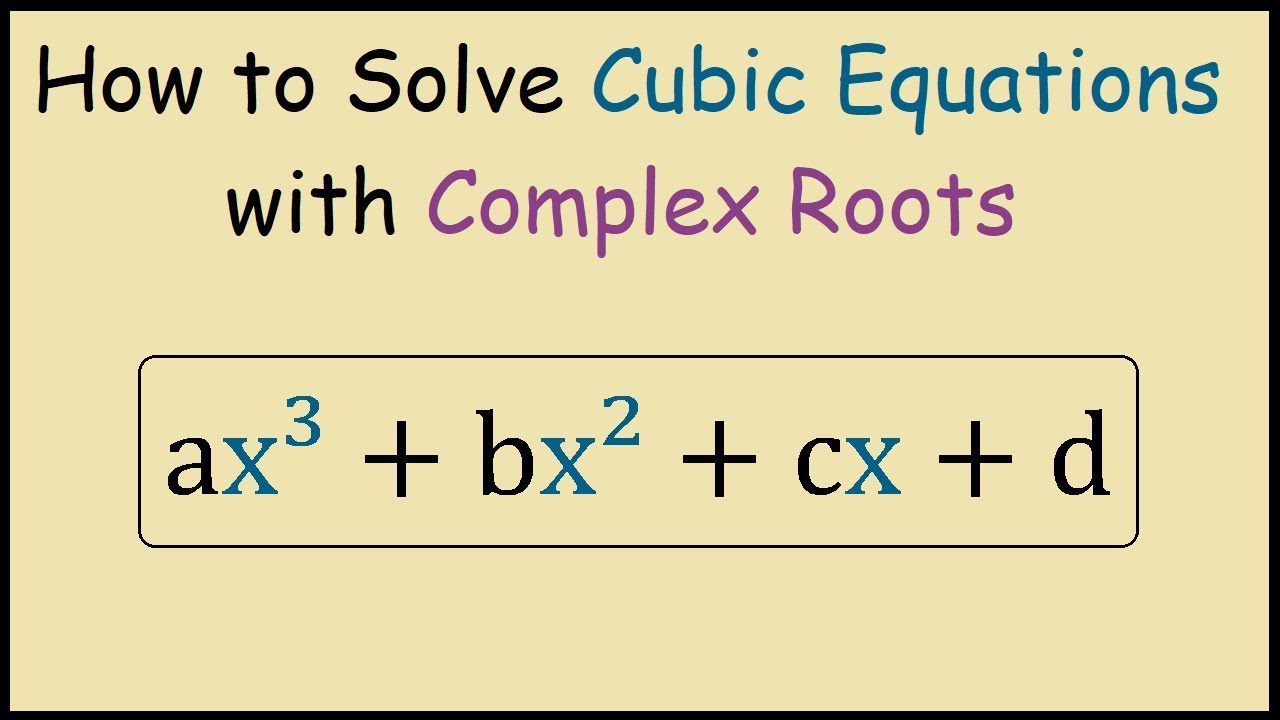
Показать описание
Learn the steps required to solve a cubic equation which has one real and two complex roots.
Begin solving our cubic equation by applying the rational roots theorem, this will find us a rational root (if any exist) which we can then use to factor out of our cubic equation through long division. This will reduce our cubic problem to a quadratic which has the same roots as our original cubic equation and give us our remaining two complex roots when solved.
Music by Adrian von Ziegler
Begin solving our cubic equation by applying the rational roots theorem, this will find us a rational root (if any exist) which we can then use to factor out of our cubic equation through long division. This will reduce our cubic problem to a quadratic which has the same roots as our original cubic equation and give us our remaining two complex roots when solved.
Music by Adrian von Ziegler
How to Solve Advanced Cubic Equations: Step-by-Step Tutorial
Solve any Cubic Equations | Cardano's Method |
Simple way to solve a cubic equation
Solving Cubic Equation [ factoring by grouping]
Factor and Solve Cubic Equations in Less Than One Minute! - Super Simple Trick
How to factor a cubic function
Solving Cubic Equations (factoring)
500 years of NOT teaching THE CUBIC FORMULA. What is it they think you can't handle?
A tricky Harvard Exam Question | Nice Exponents Math Simplification k=?
polynomials super trick to find roots of cubic equation | factorisation trick
solving a cubic equation by completing the cube
Solving a simple cubic equation. A trick you should know!
CUBIC EQUATION FACTORIZATION SHORTCUT/ SOLVING CUBIC EQUATIONS IN 10 SECONDS/ Math Tricks.
Learn how to solve a rubik's cube 3x3 in 1 minute
Can you solve this cubic equation by factoring?
How To Solve Cubic Equations
Cubic Formula for Depressed Cubic
CUBIC EQUATION FACTORIZATION SHORTCUT/ SOLVING CUBIC EQUATIONS IN 5 SECONDS - Short Trick By GP Sir
How to prove the cubic formula (from scratch)
✅ CUBIC EQUATION solved SMART in 20 seconds🏃 #equations #maths #shorts
Factorising cubic functions: The kx method
Solving Simple Cubic Equations
Solving General Cubic Equations
Solving a Cubic equation Using an Algebraic Trick
Комментарии
 0:10:52
0:10:52
 0:04:20
0:04:20
 0:04:56
0:04:56
 0:01:00
0:01:00
 0:07:18
0:07:18
 0:04:45
0:04:45
 0:03:32
0:03:32
 0:36:58
0:36:58
 0:10:58
0:10:58
 0:01:00
0:01:00
 0:07:28
0:07:28
 0:06:41
0:06:41
 0:12:06
0:12:06
 0:00:08
0:00:08
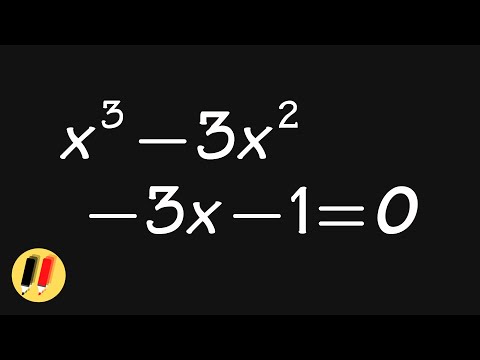 0:00:59
0:00:59
 0:09:29
0:09:29
 0:14:24
0:14:24
 0:04:52
0:04:52
 0:40:16
0:40:16
 0:00:21
0:00:21
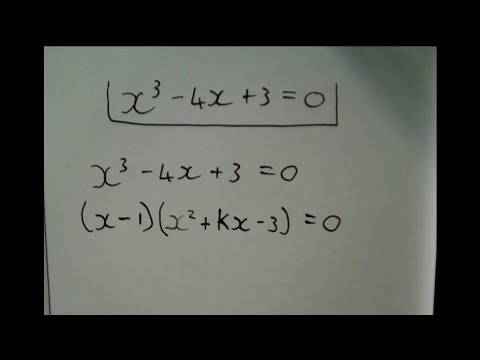 0:10:22
0:10:22
 0:09:13
0:09:13
 0:08:59
0:08:59
 0:11:45
0:11:45