filmov
tv
Theorem || if f and g are bounded function on [a,b] || riemann integral || bsc msc mathematics

Показать описание
#riemannintegral #realanalysis #bsc #gate #msc
Riemann integral, Theorem of Riemann integral
These are Riemann integration and Lebesgue integration.
Of these two Riemann integration is simpler and this is the one we look at here.
There are multiple equivalent ways of defining the Riemann integral.
The one we will look at in this video is called the Darboux definition.
The Darboux definition is easier to work with and prove things with than the original definition that Riemann first used, but is ultimately equivalent to the original Riemann definition.
We explain and motivate this definition in the video and also give an example of proving a function is Riemann integrable over an interval and o different example of proving a function isn’t Riemann integrable over an interval.
Contents:
Part 1 - Definition of a dissection/partition
Parts 2 to 4 - Riemann Sums
Part 5 - Definition of Riemann Integration
Part 6 - Example of proving a function is Riemann Integrable
Riemann integral, Theorem of Riemann integral
These are Riemann integration and Lebesgue integration.
Of these two Riemann integration is simpler and this is the one we look at here.
There are multiple equivalent ways of defining the Riemann integral.
The one we will look at in this video is called the Darboux definition.
The Darboux definition is easier to work with and prove things with than the original definition that Riemann first used, but is ultimately equivalent to the original Riemann definition.
We explain and motivate this definition in the video and also give an example of proving a function is Riemann integrable over an interval and o different example of proving a function isn’t Riemann integrable over an interval.
Contents:
Part 1 - Definition of a dissection/partition
Parts 2 to 4 - Riemann Sums
Part 5 - Definition of Riemann Integration
Part 6 - Example of proving a function is Riemann Integrable
Differentiable then Continuous Proof
Fundamental Theorem of Calculus Part 1
Rolle's Theorem
Mean Value Theorem
Theorem on continuity of function | Metric Space | Real analysis
Boundedness Theorem (W/Voice Explanation) Proof | Maths |Mad Teacher
Theorem|A Function is Continuous iff For Any Subset of Y inverse(intA) is Subset of int[inversef(A)]
Intermediate Value Theorem | Fixed Point Theorem | Use IVT to prove Fixed Point | Calculus - Part 5
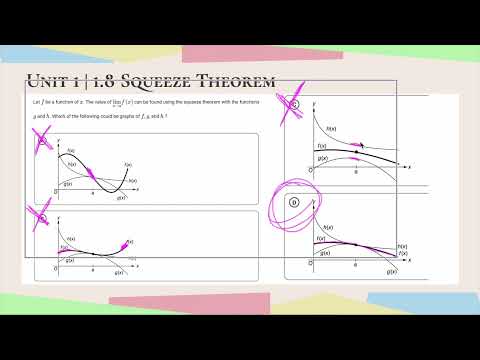
Squeeze Theorem MCQ | AP Calculus Topic 1.8
Continuity of function | Theorem | f is Continous iff f (Ā) is subset closure of f(A) | metric space...
Rouche's Theorem with Example | Complex Analysis #23
Every continuous function is Riemann Stieltjes Integrable | Theorem
lec#20.Calc.Theorem#Prove Differentiability implies continuity but the converse is not always true .
Theorem || If K/F is an extension of F and a is algebraic over F iff [F(a): F ]=n || Field Theory
Theorem || if f and g are bounded function on [a,b] || riemann integral || bsc msc mathematics
If f is bounded & has a finite no. of points of discontinuity on [a,b] then f is integrable on [...
Find Maximum Value of Function from Mean Value Theorem Application Calculus 2
A Function from X to Y is Continuous iff for every open set V in Y f–1(V) is open in X
Continuous implies Bounded
If f is bounded variation on [a,b] then it is also bounded variation on [a,c] and [c,b].
FUNCTION THEOREM-1 g o f is bijection theorem
How to determine if a factor is a factor of a polynomial using factor theorem
Continuity 9 || Boundednes theorem || if f is continuous in [a,b] then f is bounded in [a,b]|| Math
Remainder theorem: find k if f(x)=x^2+kx-20
Комментарии
 0:03:51
0:03:51
 0:11:30
0:11:30
 0:19:32
0:19:32
 0:19:40
0:19:40
 0:19:25
0:19:25
 0:06:42
0:06:42
 0:07:36
0:07:36
 0:14:15
0:14:15
 0:09:14
0:09:14
 0:14:57
0:14:57
 0:04:33
0:04:33
 0:15:04
0:15:04
 0:03:28
0:03:28
 0:44:29
0:44:29
 0:08:01
0:08:01
 0:21:52
0:21:52
 0:05:41
0:05:41
 0:12:58
0:12:58
 0:08:11
0:08:11
 0:11:30
0:11:30
 0:12:15
0:12:15
 0:02:56
0:02:56
 0:22:31
0:22:31
 0:01:24
0:01:24