filmov
tv
A Quick and Easy Cubic Equation | Algebra

Показать описание
🤩 Hello everyone, I'm very excited to bring you a new channel (SyberMath Shorts).
Enjoy...and thank you for your support!!! 🧡🥰🎉🥳🧡
If you need to post a picture of your solution or idea:
x^3-8x=8
#PolynomialEquations #Polynomials
via @YouTube @Apple @Desmos @NotabilityApp @googledocs @canva
PLAYLISTS 🎵 :
Enjoy...and thank you for your support!!! 🧡🥰🎉🥳🧡
If you need to post a picture of your solution or idea:
x^3-8x=8
#PolynomialEquations #Polynomials
via @YouTube @Apple @Desmos @NotabilityApp @googledocs @canva
PLAYLISTS 🎵 :
Simple way to solve a cubic equation
A Quick and Easy Cubic Equation | Algebra
Can You Solve this Cubic Equation in 1 Minute? | Quick & Simple Explanation
Factor and Solve Cubic Equations in Less Than One Minute! - Super Simple Trick
Solving a simple cubic equation. A trick you should know!
Solve this Cubic Equation | Fast & Easy Method
Solve Cubic Equations - Quick and Simple Factoring Method
How to Solve Cubic Equations by Factoring | Simple and Easy Tutorial
Planar density of simple cube plane (111)
Factor & Solve these Cubic Equations in Less Than a Minute | Easy Step-By-Step Tutorial
Solving Simple Cubic Equations
How to Factor and Solve Cubic Equations in Less Than ONE Minute - Quick and Easy Trick
Solve this Cubic Equation Using NO FUSS FACTORS | Fast & Easy Method
How to Factor and Solve Cubic Equations in Less Than a Minute | Quick & Simple Explanation
Planes of simple cubic system
Solve Cubic Equations - Simple Factoring Method
Can You Factor and Solve This Cubic Equation In Under a Minute? - Simple Math Trick
Factorising cubic functions: The kx method
He can factor a cubic trinomial
Unit Cell Chemistry Simple Cubic, Body Centered Cubic, Face Centered Cubic Crystal Lattice Structu
500 years of NOT teaching THE CUBIC FORMULA. What is it they think you can't handle?
Simple wood log calculate method#cubic feet calculate method#shorts#furniture#teakwood#shorts
Solving difficult Cubic Equations Short Trick - Super Shortcut Method
How to convert volume liter to cubic meter | Liter to cubic metre #shorts #short #trend #fun #cbse
Комментарии
 0:04:56
0:04:56
 0:09:33
0:09:33
 0:02:52
0:02:52
 0:07:18
0:07:18
 0:06:41
0:06:41
 0:05:46
0:05:46
 0:04:03
0:04:03
 0:04:55
0:04:55
 0:18:15
0:18:15
 0:09:03
0:09:03
 0:09:13
0:09:13
 0:06:26
0:06:26
 0:07:22
0:07:22
 0:09:17
0:09:17
 0:05:18
0:05:18
 0:06:15
0:06:15
 0:08:46
0:08:46
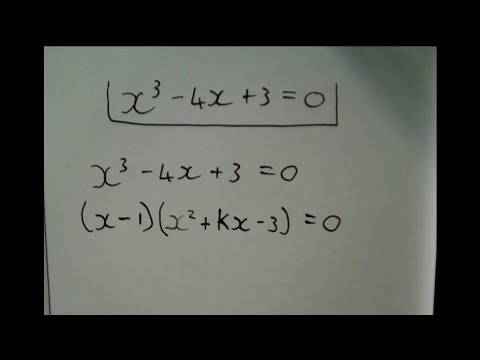 0:10:22
0:10:22
 0:00:14
0:00:14
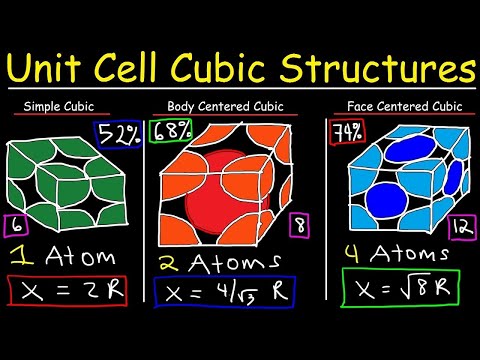 0:17:22
0:17:22
 0:36:58
0:36:58
 0:00:26
0:00:26
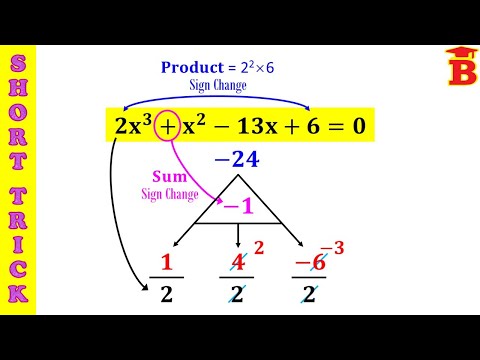 0:04:34
0:04:34
 0:00:15
0:00:15