filmov
tv
The Big Theorem, Part I

Показать описание
Learning Objectives:
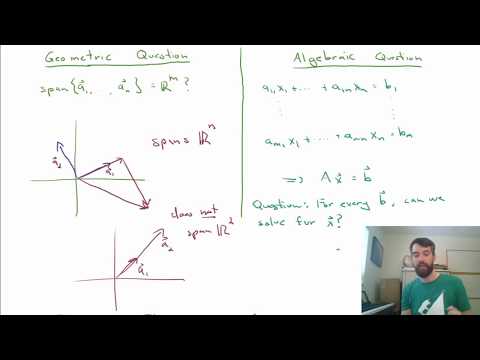
1) State the two major problems: one geometric, one algebraic
2) State the Big Theorem, which compares span, linear combinations, and the REF form of a matrix
3) Prove the Big Theorem formally
This video is part of a Linear Algebra course taught at the University of Cincinnati.
1) State the two major problems: one geometric, one algebraic
2) State the Big Theorem, which compares span, linear combinations, and the REF form of a matrix
3) Prove the Big Theorem formally
This video is part of a Linear Algebra course taught at the University of Cincinnati.
The Big Theorem, Part I
One-to-one, Onto, and the Big Theorem Part II
The Big Theorem of Differential Equations: Existence & Uniqueness
11.7 The Big Theorem
11.8 Proof of the 'Big Theorem'
When does a matrix fail to be invertible? Also more 'Big Theorem'.
Fundamental Theorem of Calculus Explained | Outlier.org
Fundamental theorem of calculus (Part 1) | AP Calculus AB | Khan Academy
PDSA-Week-2-Problem Solving Session(Coding)
Proving Fermat' s Last Theorem (almost) in just 2 minutes !
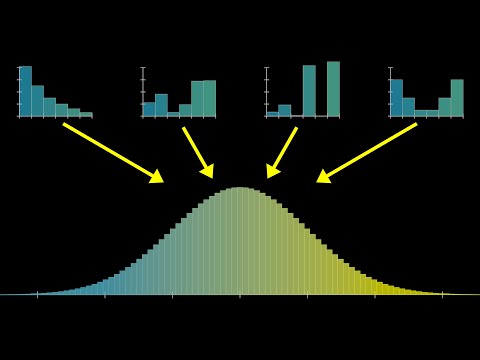
But what is the Central Limit Theorem?
The Beginning of Everything -- The Big Bang
23 - The Binomial Theorem & Binomial Expansion - Part 1
Calculus 1 Lecture 4.5: The Fundamental Theorem of Calculus
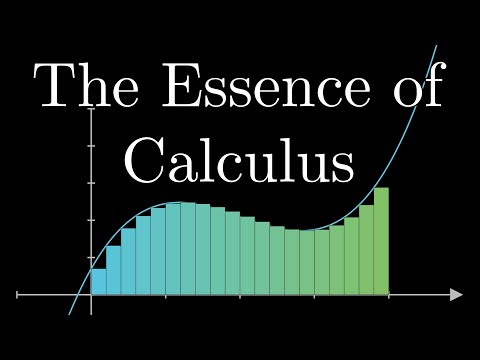
The essence of calculus
Fundamental Theorem of Calculus 1 | Geometric Idea + Chain Rule Example
Solving Circle Theorem Questions | Maths GCSE
Fermat's Last Theorem - Numberphile
The Fundamental Theorem of Calculus: Redefining Integration
A generalized BDF-Kasparov theorem and Voiculescu theorem, Part I
Bayes theorem, the geometry of changing beliefs
The Second Fundamental Theorem of Calculus
Understand WHY the Pythagorean Theorem is True - Nice Visual Proof
Metaphysical Implications Of Godel's Incompleteness Theorem - Part 1
Комментарии
 0:14:01
0:14:01
 0:09:30
0:09:30
 0:12:22
0:12:22
 0:05:01
0:05:01
 0:05:31
0:05:31
 0:08:45
0:08:45
 0:16:27
0:16:27
 0:08:03
0:08:03
 3:07:26
3:07:26
 0:02:00
0:02:00
 0:31:15
0:31:15
 0:05:55
0:05:55
 0:34:02
0:34:02
 2:46:09
2:46:09
 0:17:05
0:17:05
 0:11:04
0:11:04
 0:00:59
0:00:59
 0:09:31
0:09:31
 0:09:38
0:09:38
 0:49:35
0:49:35
 0:15:11
0:15:11
 0:05:22
0:05:22
 0:01:00
0:01:00
 2:02:45
2:02:45