One-to-one, Onto, and the Big Theorem Part II

Показать описание

Learning Objectives:
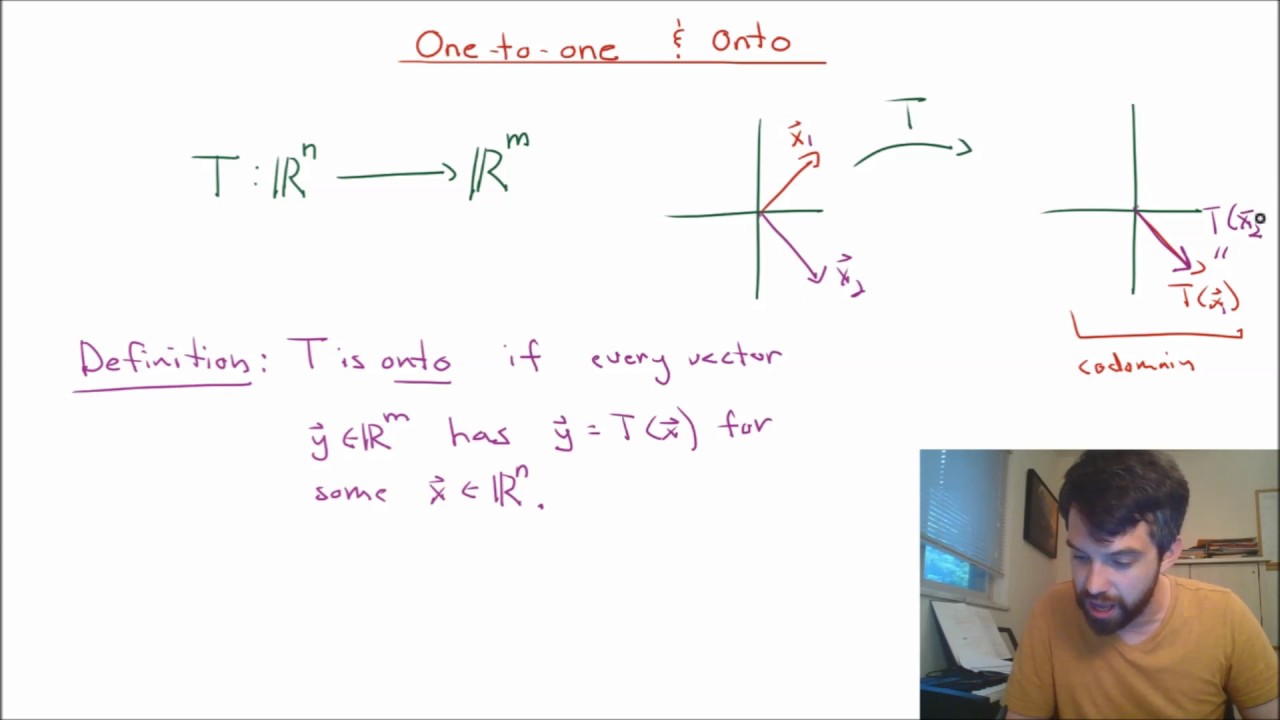
1) Define one-to-one and onto
2) Given a matrix, decide whether it is one-to-one or onto
3) Find equivalent properties to a transformation being onto (or one-to-one)

This video is part of a Linear Algebra course taught at the University of Cincinnati.

BECOME A MEMBER:

MATH BOOKS & MERCH I LOVE:

Рекомендации по теме

Комментарии

The first 30 simple, clear, and concise videos - each on average 10 minutes, adding up to approximately 300 minutes ~ 5 hours - bring together seemingly different ideas in linear algebra in such a way that NO BOOK ON THIS PLANET CAN DO THE SAME JOB by reading that book for five hours. Every single video of yours deserve to be liked. Thank you for all the time and effort you have put in creating the Linear Algebra playlist. I really hope that all of you other playlists have this same incredible effect in them.

mostafaahmadi

No one has ever explained visually about 1-1 and onto like you did! Before I watched your video, I just knew that 1-1 that A is linear independent, but now I understand why. You did a great job! Thank you so much!

NguyenHaNhutLong

Thanks a lot, best Linear algebra course on internet

mayanknaithani

Thanks for the help man. Passed my quiz because of you.

IzzyP

I think one-to-one is called injection in french and onto is called surjection.

youssefdirani

Condition 4 is equivalent to there being no zero rows for REF A or RREF A .
I assume that it does not matter if REF A or RREF A is used here.
So R(R)EF A having no zero rows implies Ax = b is onto, for all b.
Since if there was a zero row we have the inconsistent augmented matrix
* * * * * *
[0 0 0 ... 1], thus not all b's are mapped to by T(x), namely all the b vectors which have a nonzero element in its final component.

The one-to-one type Ax =b would probably occur when every column in A is a pivot column, i.e. there are no 'free variable' columns.

xoppa

One-to-one, Onto, and the Big Theorem Part II

One-to-one, Onto, and the Big Theorem Part II

One to one, onto, matrix

Linear Algebra: Checking if a transformation is one-to-one and onto

Proving a Function is One-to-One and Onto

How to tell the difference between onto and one to one functions

Determine if a Linear Transformation is One-to-One and/or Onto (R3 to R2)

Functions, Domain, Codomain, Injective(one to one), Surjective(onto), Bijective Functions

Onto and One-to-One Mappings (Example)

Determining whether a transformation is onto | Linear Algebra | Khan Academy

The Kiffness x Oh Long Johnson 2.0 - Hold Onto My Fur (Talking Cat Song)

One-to-one and Onto Linear Transformations

One Piece 778 ENG SUB | Carrot Sneaks onto Sunny headed to Big Mom Headquarters

One to One Function (Injection) | Injective Function

Horror moment HUGE spider climbs onto sleeping baby #Shorts 😱 🕷

We got into our first big fight on camera... (new baby?)

Determine if Transformation Mappings Are One-to-One and/or Onto

This Women Haul A 450kg Bluefin Tuna Onto Her Boat, Solo!

Prove Composition of One-to-One and Onto Functions is One to One and Onto

Big Floppy Saint Bernard Pup trying to climb onto a bed. 😂#funnydogvideo #dogshorts #funnyshorts

I Found a Secret Pond Full of Monsters!

Into or onto - it makes a big difference 🙃 #englishlearning #vocabulary #ielts

BIG ANIME SEQUELS ANNOUNCED✅

Little Boy Falls Onto Grass While Running to Catch School Bus

How Deep Into The Earth Will This Go from 1000ft?