The Fundamental Theorem of Calculus: Redefining Integration

Показать описание

So we know a lot about differentiation, and the basics about what integration is, so what do these two operations have to do with one another? Everything! And the discovery of their relationship is what launched modern calculus, back in the time of Newton and pals. Check it out!

Check out "Is This Wi-Fi Organic?", my book on disarming pseudoscience!

Рекомендации по теме

Комментарии

I am 72 years old and enjoy substituting in high school science and math classes. I am in the process of teaching myself calculus. I have an appreciation of limits and derivatives but want to understand how and why integration works. Every video I have watched (and I have watched plenty) showed how to perform integration but none in a manner that made me feel that I really understood the concept. This is the best explanation I have seen thus far. Math books labor over formulas and some videos seem to want you to accept the concept because it is so. The implication being, if you do not understand, it is because you are either not trying hard enough or just not bright enough. This video really want us to understand integration. Thank you. For those still struggling with it, relax and do not stress. Watch it again, in a couple of days. Your subconscious mind will work on it, in between views. If a 72 year old can get it, you can too.

thomasjohnson

I can't thank you enough for your colossal contribuation to my understanding of maths and physics. I'm a medicine doctor but I'm fascinated by physics and chemistry. I've read a dozen books about physics but the authors focused on the equations and the formulas rather than the phenomena themselves. Your videos are way better. Thank you again.

adleneboulebtateche

The "dx" actually does have a purpose. It is delta-x from the summation, in the limit as n -> infinity. It is the "width" of a "slice" of the region under the curve, which when multiplied by f(x), the "height", gives us the area of the slice.

KenSchwartzMath

Accepting an idea that I don't actually understand is stress.

You're saving and transforming lives.
God bless you Prof🙏

derrickwright

We are the same age more or less. I studied electronics engineering while hated math all my life. Just decided to binge watch all math from start to finish. With a different viewpoint and mostly with this amazing presentation, calm voice, would love it as should. Thanks for the inspiration.

apostolosfilippos

dx does have a meaning! It means "a little bit of x" as change in x approaches 0. It is the width of the rectangle. Now, dy/dx = f(x), so dy=f(x)dx. The Sum (integral) of dy, then, is the Sum (integral) of f(x)dx, which equals y + C.

andrew

I cannot even begin to express how thankful I am to have you as a resource, it feels good to actually understand something. Thanks for doing what you do, Prof Dave!

NopeChuckTesla

Watched a 2 hour lecture on this, did not understand a single thing. Watched 9 minutes of this video and it instantly cleared up the doubts I had. Thank you!

muffledd

So many people told me calculus was hell and hard. But since this is extremly easy for me, it must be the great teacher dave

AlexanderSchwarz-ckcx

If you are a varsity student like me and the textbooks and lectures weren't helping so youtube brought you here, you are safe, just continue watching the series. Thank you Dave.

Teddy_on_yt

Yes but why does the antidervitive gives you the area under the curve

SENA

Can't thank you enough . I've spent entire days trying to self study and search online explanations but you're video explained everything in less than 20mins

jmt

Thank you sir for your dedication and for making this free! 🙏

Kiky_MedPhysicist

Still don't get it....😓😭 I wish I was smart matematically.
I will continue watching, maybe one day I will have my Eureka moment!
Thanks Prof.Dave.

aniawo

This is one of those videos where it just snaps into place in your brain, "I understand calculus". Officially feel like neo when he said " I know kung-fu".

benno

Will need this for next semester when I take Calc! Good stuff as always

papermario

It is incredible that such a concept didn't exist for millenairies until Newton and Leibniz discovered it.

Muck-qyoo

Tell how prof Dave gave me a better understanding of the FTC than my professors that I pay to teach me. Thanks so much, I think I might pass Math now :)

jennawalker

this is good stuf. my math school teacher illegally didn't teach us everything and now i'm in college trying to learn this for the first time, way after than it should've been
but i was only able to understand it now, THANK YOU DAVE

miss_B_

I call it the derivative ladder. Once you think of a list of functions that way, you're all set.

fortundiamond

The Fundamental Theorem of Calculus: Redefining Integration

Fundamental Theorem of Calculus Part 1

Integration and the fundamental theorem of calculus | Chapter 8, Essence of calculus

Fundamental theorem of calculus (Part 1) | AP Calculus AB | Khan Academy

The Fundamental Theorem of Calculus: Redefining Integration

Calculus 1 Lecture 4.5: The Fundamental Theorem of Calculus

Fundamental Theorem of Calculus - Part I

Fundamental Theorem of Calculus Explained | Outlier.org

Fundamental Theorem of Calculus 1 | Geometric Idea + Chain Rule Example

Mathematics - Fundamental Concepts of Solution of Triangles (SOT) Part-1 | Foundation Series

3 Levels of Proving the Fundamental Theorem of Calculus | #SoME3

Fundamental Theorem of Calculus Part 2

What is the Fundamental Theorem of Calculus?

The Fundamental Theorem of Calculus - Full Tutorial

Real Analysis | The Fundamental Theorem of Calculus

Integrals | Fundamental Theorem of Calculus | Part 1

Proof of fundamental theorem of calculus | AP Calculus AB | Khan Academy

Calculus 1: The Fundamental Theorem of Calculus (Section 5.3) | Math with Professor V

Fundamental Theorem of Calculus Parts 1&2

Math 2B. Calculus. Lecture 04. The Fundamental Theorem of Calculus.

Fundamental Theorem of Calculus (1 of 5: Considering COVID-19)

Fundamental Theorem of Calculus II

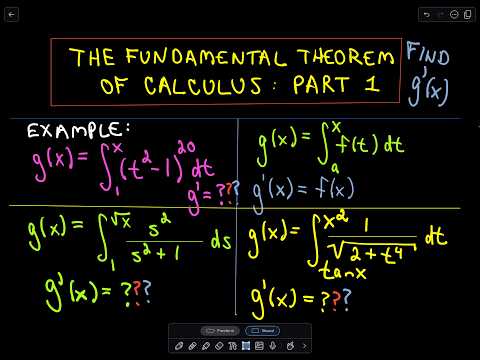
Fundamental Theorem of Calculus Part 1

Calculus AB/BC – 6.4 The Fundamental Theorem of Calculus and Accumulation Functions

Real Analysis 56 | Proof of the Fundamental Theorem of Calculus