filmov
tv
“Adding” Scalars and Bivectors: Ridiculous?! A video for high-school teachers of Geometric Algebra

Показать описание
High-school teachers will be key players in the spread of Geometric Algebra. Providing these teachers with the background to answer students' questions is an important task for us. Here's a high-school-level answer to an objection/question that intelligent students are likely to raise.
LinkedIn group "Pre-University Geometric Algebra"
The group is a space for the sharing and collaborative development of resources for teaching GA at the high-school level. More-advanced materials are welcome, especially if prepared with the additional intent of helping high-school students develop the abilities needed to understand and do such work themselves within a few years.
Document "About the "Addition" of Scalars and Bivectors in Geometric Algebra"
ABSTRACT
“You can’t add things that are of different types!” This objection to the “addition” of scalars and bivectors—which is voiced by physicists as well as students—has been a barrier to the adoption of Geometric Algebra. We suggest that the source of the objection is not the operation itself, but the expectations raised in critics’ minds by the term “addition”. Indeed, the ways in which this operation interacts with others are unlike those of other “additions”, and might well cause discomfort to the student. This document explores those potential sources of discomfort, and notes that no problems arise from this unusual “addition” because the developers of GA were careful in choosing the objects (e.g. vectors and bivectors) employed in this algebra, and also in defining not only the operations themselves, but their interactions with each other. The document finishes with an example of how this “addition” proves useful.
LinkedIn group "Pre-University Geometric Algebra"
The group is a space for the sharing and collaborative development of resources for teaching GA at the high-school level. More-advanced materials are welcome, especially if prepared with the additional intent of helping high-school students develop the abilities needed to understand and do such work themselves within a few years.
Document "About the "Addition" of Scalars and Bivectors in Geometric Algebra"
ABSTRACT
“You can’t add things that are of different types!” This objection to the “addition” of scalars and bivectors—which is voiced by physicists as well as students—has been a barrier to the adoption of Geometric Algebra. We suggest that the source of the objection is not the operation itself, but the expectations raised in critics’ minds by the term “addition”. Indeed, the ways in which this operation interacts with others are unlike those of other “additions”, and might well cause discomfort to the student. This document explores those potential sources of discomfort, and notes that no problems arise from this unusual “addition” because the developers of GA were careful in choosing the objects (e.g. vectors and bivectors) employed in this algebra, and also in defining not only the operations themselves, but their interactions with each other. The document finishes with an example of how this “addition” proves useful.
Комментарии
 0:19:13
0:19:13
 0:19:13
0:19:13
 0:44:23
0:44:23
 0:54:38
0:54:38
 0:38:13
0:38:13
 0:37:22
0:37:22
 0:51:16
0:51:16
 0:09:15
0:09:15
 0:23:28
0:23:28
 0:11:24
0:11:24
 0:57:08
0:57:08
 0:56:36
0:56:36
 1:03:51
1:03:51
 0:11:24
0:11:24
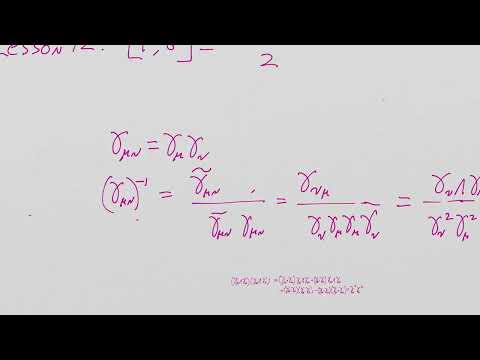 0:49:30
0:49:30
 0:44:10
0:44:10
 0:58:11
0:58:11
 0:57:23
0:57:23
 0:55:15
0:55:15
 0:13:57
0:13:57
 0:07:11
0:07:11
 0:21:35
0:21:35
 0:40:35
0:40:35
 0:31:27
0:31:27