QED Prerequisites Geometric Algebra 5- Multivectors

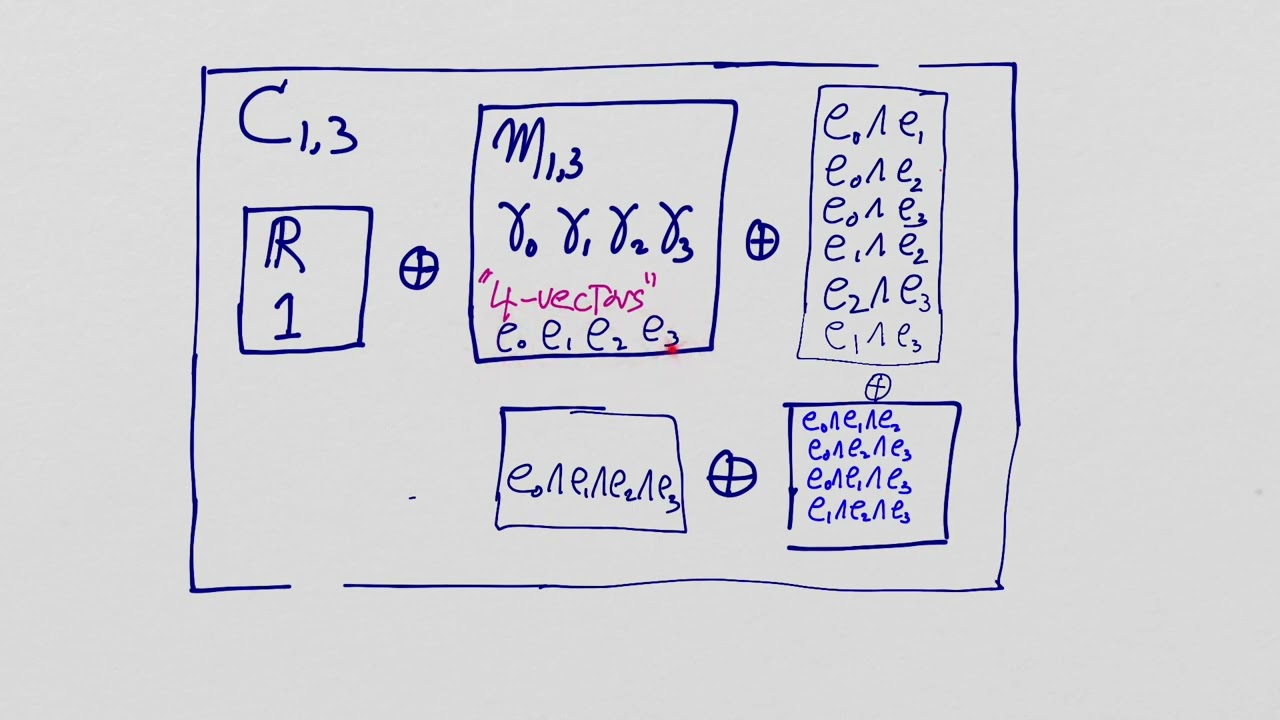
In this lesson we introduce the idea of multivectors and emphasize the need to understand how to take the spacetime product of any two multivectors in the Spacetime Algebra. We demonstrate how this is done for the product between a vector and a bivector and we interpret the meaning of each part of the resulting multivector.

The software I usually use to produce the lectures is:

[Nickle]

Well that's my evening sorted out ... :-)

[leodorst]

A k-blade is a k-vector that can be written as a wedge product of k 1-vectors. It is factorizable. Not all k-vectors are, in 4D or more. Only blades can be interpreted geometrically as oriented subspaces, so the term is important to keep straight.

[monadic_monastic]

Around at 13:00 I'm pretty sure the authors made a bit of a typo and didn't intend to also call the wedge/outer product "non-associative" since I don't think that's ever true.

Regarding the inner product, I think it may seem they're just deeming the dot product non-associative because of a similar reasoning of it being defined only between two vectors, but I have a sneaking suspicion the authors are leaning on intuition from other places. There's a related concept to the inner product called "(left/right) contraction" in the GA community (c.f. "Geometric Algebra for Physicists" or "the inner products of geometric algebra") which turns out to be totally non-associative, or the "interior product" in exterior algebra of diff. forms, which I *think* is also non-associative? For two reasons:

1. a similar argument used to why the geometric algebra left/right contraction is non-associative you might call "grade chasing" (lmao): the interior product is a map from say, p forms to p-1 forms right? But i can't just willy-nilly turn that into a left-contraction on one of the individual wedge-products of the p form, making it a map from say a p-r form to a p - r - 1 form. (this might be a little hard to picture, maybe a comparison would be to compare with the grade-raising wedge product, which can either be viewed as a p -> p+1 map, or a (1 + 1) + (p -1) map, etc... due to its associativity)

2. The fact that the non-associative GA left/right contraction satisfies the same adjoint relation to the wedge product as the interior product does (and why I suspect they're in fact the same?)

[monadic_monastic]

Also would you say Clifford/Geometric Algebra (specifically its multivector basis elements) represent the degrees of freedom (in the mechanics sense) that you're allotted when fed what spatial dimensions you're working in? (and then specific GA products tell you what products/actions in this algebra correspond to some specific configuration in space? Or in other words what degrees of freedoms are involved in it, in the same way regular vector spaces - if representing something with spatial meaning - tell you how much of the regular old 3 spatial dimensions are involved)

For example, if I feed geometric algebra a 3D vector space, then what it gives me back is an algebra that contains 8 basis elements, 6 of which gives you the x, y, z elements, but then also the roll/yaw/pitch degrees of freedom as well (I do not know yet how to interpret both the scalar and the volumetric pseudoscalar elements).

I know this is a *heavy* components-based way of interpreting elements in the algebra, when in the GA community it's encouraged to really view things "coordinate-free", but I also like to see if it's totally compatible with this other perspective as well (and I feel like it helps clear up old worries I've had since the beginning about what adding a real number to an imaginary number was "really" representing/modelling all along)

[jackozeehakkjuz]

at the end of minute 50 you write the geometric product on the left of v(e1∧e2)=(v·e1)e2-(v·e2)e1.

I guess you are probably thinking of writing the *dot* product v · (e1∧e2), since the geometric product would also include the antisymetric part v∧e1∧e2. (unless v was already contained in the plane spanned by e1 and e2, of course)

oh nvm you correct it at 54:30

[Nickle]

The reals form a subalgebra, albeit a trivial one.