filmov
tv
Example Second-Order ODE: Spring-Mass-Damper

Показать описание
This video solves an important second-order ordinary differential equation (ODEs): The damped harmonic oscillator for a mass on a spring with damping. We solve this by hand and also plot the solution in Python and Matlab.
@eigensteve on Twitter
This video was produced at the University of Washington
%%% CHAPTERS %%%
0:00 Deriving the Spring-Mass-Damper Equations from F=ma
6:46 Solve the Equation by Guessing Solution x(t) = exp(a*t)
9:35 The Characteristic Equation
14:54 Using Initial Conditions to Find Undetermined Coefficients
18:08 Writing as a Matrix System of Equations
21:12 Matlab Code Example
30:44 Python Code Example
@eigensteve on Twitter
This video was produced at the University of Washington
%%% CHAPTERS %%%
0:00 Deriving the Spring-Mass-Damper Equations from F=ma
6:46 Solve the Equation by Guessing Solution x(t) = exp(a*t)
9:35 The Characteristic Equation
14:54 Using Initial Conditions to Find Undetermined Coefficients
18:08 Writing as a Matrix System of Equations
21:12 Matlab Code Example
30:44 Python Code Example
Example Second-Order ODE: Spring-Mass-Damper
Second order differential equation for spring-mass systems
Spring mass damper system - Equations of motion
Solving second order ordinary differential equation using simulink - spring mass damper
Mechanical Vibrations: Underdamped vs Overdamped vs Critically Damped
Modeling Mass-Spring-Damper Systems - 2nd Order ODEs
Undamped Mechanical Vibrations & Hooke's Law // Simple Harmonic Motion
Free Oscillation | Application of Second Order Differential Equation (Spring-Mass System)
Second-Order Ordinary Differential Equations: Solving the Harmonic Oscillator Four Ways
Intro to Mass-Spring Oscillator (Second-Order Differential Equation)
Second-order ODE Tutorial
Application of second order diff. eq. (Mass Spring System), Free vibration system
2.3 Second-order ODE - Damped systems
PART II: SOLVING DIFFERENTIAL EQUATION OF A SPRING MASS DAMPER SYSTEM
Mechanical Vibrations 8 - Newton 2 - Double Mass-spring-damper system
Session 24: Modeling and idea on Damped Mass Spring system ( Part II).
Introduction to Spring-Mass Second Order ODE
Class 02 ODE Modeling: Spring-Mass-Damper Dynamics
Session 23: Modeling of Undamped Mass Spring system with some examples (Part I).
Class 04 ODE Alternatives: Spring Mass Damper in State Space
Runge Kutta Second order problems solved for airdrag, coulomb, spring mass damper
Coupled oscillators | Lecture 46 | Differential Equations for Engineers
3.6 part 4: Modeling Forced Damped Oscillations using Differential Equations
Class 03 Laplace Transform: [Activity] Spring-Mass-Damper Transfer Function *
Комментарии
 0:33:00
0:33:00
 0:36:24
0:36:24
 0:04:32
0:04:32
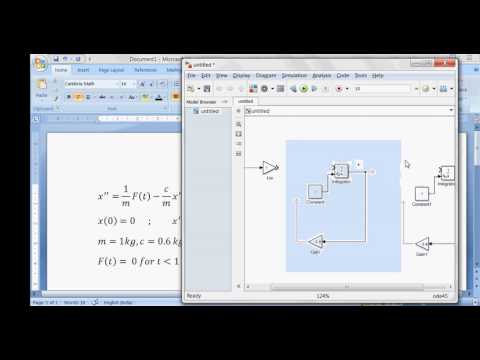 0:09:20
0:09:20
 0:11:16
0:11:16
 0:21:00
0:21:00
 0:08:10
0:08:10
 0:16:13
0:16:13
 0:37:02
0:37:02
 0:07:52
0:07:52
 0:17:24
0:17:24
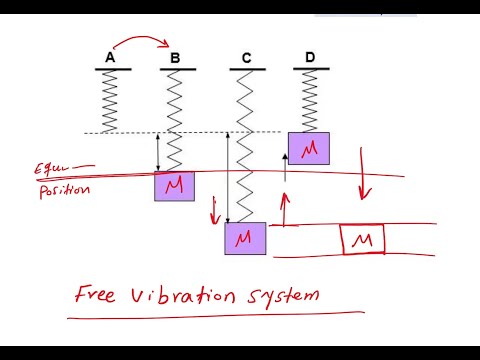 0:12:41
0:12:41
 0:07:06
0:07:06
 0:27:52
0:27:52
 0:12:00
0:12:00
 0:07:45
0:07:45
 0:59:55
0:59:55
 0:09:07
0:09:07
 0:18:42
0:18:42
 0:05:47
0:05:47
 0:12:08
0:12:08
 0:09:43
0:09:43
 0:08:00
0:08:00
 0:10:06
0:10:06