Newton's laws in polar coordinates | Classical Mechanics

preview_player
Показать описание
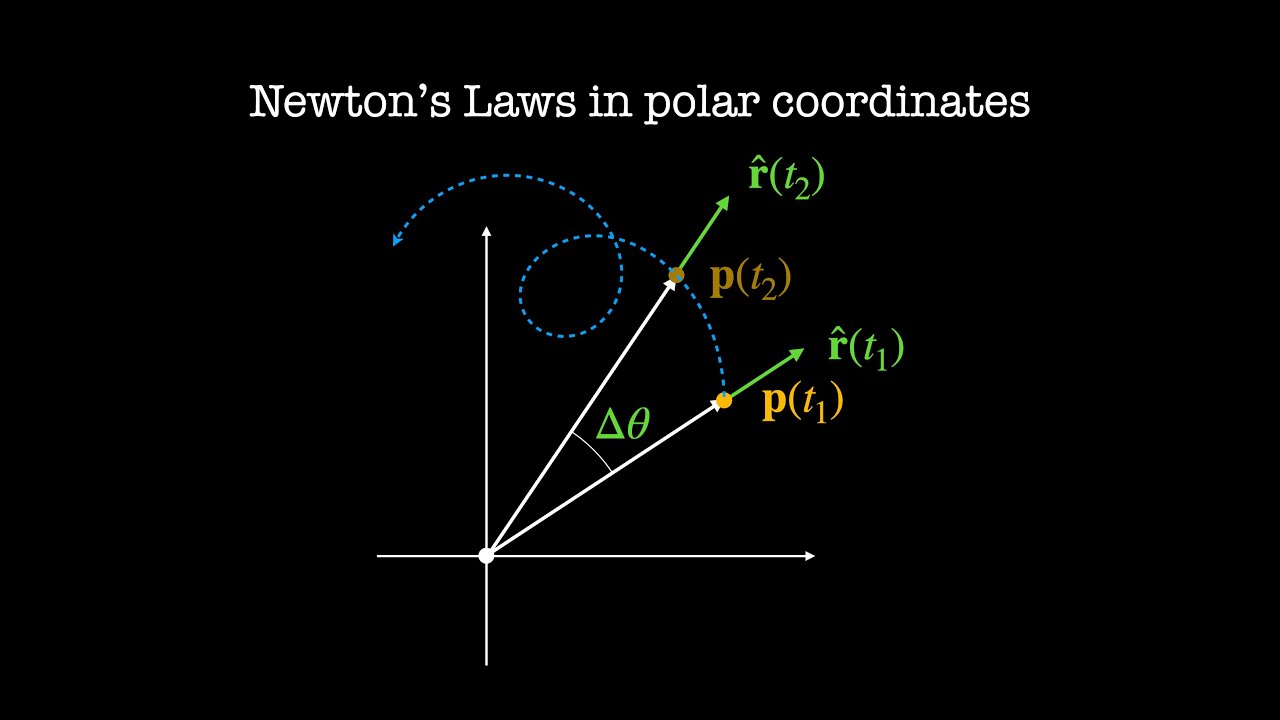
Polar coordinates are useful for solving physics problems with circular symmetry. Here, we derive the calculus and math needed to write F=ma in polar coordinates, which lets us solve problems where forces can act radially and tangentially.

Music "Everything" by Vi Hart
  1. Sabetta Talks Math
Рекомендации по теме
Newton's laws in 0:06:52

Newton's laws in polar coordinates | Classical Mechanics

Deriving Newton's Second 0:10:35

Deriving Newton's Second Law in Polar Coordinates (Part 1)

Newton's Laws in 0:29:16

Newton's Laws in Polar Coordinates

Newton's Second Law 0:24:44

Newton's Second Law in Polar Coordinates | Classical Mechanics

Newtons law in 0:15:46

Newtons law in polar coordinate

Lecture 9 - 0:44:41

Lecture 9 - Newton's laws of motion in polar coordinates

Newton's 2nd Law 0:08:07

Newton's 2nd Law Polar and Cylindrical Coordinates

Classical Mechanics: Newton’s 0:27:53

Classical Mechanics: Newton’s Second Law in Polar Coordinates

Examples Newton's Second 0:16:31

Examples Newton's Second law Polar System

Newtons 2nd law 0:12:27

Newtons 2nd law in polar coordinate system

Solving Newton’s equations 0:26:24

Solving Newton’s equations of motion in Polar Coordinates | Engineering Physics | JNTU

Dynamics: Particle Kinetics, 0:17:12

Dynamics: Particle Kinetics, Newtons 2nd Law Polar Coordinates Example (ES211 Class 7)

L07.3 - Dynamics 0:10:50

L07.3 - Dynamics - Lesson 7.3 - Newton's 2nd Law with Cylindrical coordinates

Dynamics 2nd Law 0:05:15

Dynamics 2nd Law Polar Coordinates Example 2

Unit-1 EP: Polar 0:25:02

Unit-1 EP: Polar coordinates|Equation of motion in Polar coordinates|b tech first year

Curvilinear Motion Polar 0:07:26

Curvilinear Motion Polar Coordinates (Learn to solve any question)

Velocity, Acceleration in 0:23:41

Velocity, Acceleration in Polar Coordinates

Newton’s second law 0:20:18

Newton’s second law in polar coordinates

Pendulum in Polar 0:18:46

Pendulum in Polar Coordinates: Equations of Motion

Orbital Motion in 0:19:52

Orbital Motion in Polar Coordinates

Analyzing a pendulum 0:15:58

Analyzing a pendulum using Newton's laws in polar coordinates

F=ma Cylindrical Coordinates| 0:11:08

F=ma Cylindrical Coordinates| Equations of Motion| Learn to solve any problem

Polar Coordinate 0:10:11

Polar Coordinate

11.1 Newton's 2nd 0:03:17

11.1 Newton's 2nd Law and Circular Motion

Комментарии
Автор

Amazing videos!, Saving fellow undergrads like us who just need a little push in the right direction of math🙌🔥

vize_vids
Автор

Beautiful explanation as usual, Sabetta!
We’ve only seen Rigid Bodies so far; however, if I’m not mistaken, your area of research is in soft bodies too.
Wouldn’t it be great to see some videos about Continuum Mechanics/Elasticity Theory/non-Rigid Bodies too? It’s undoubtedly the topic I understood the least in my Undergraduate studies.
You’re great! Keep ‘em coming!

MsSlash
Автор

At 2:56 I can't understand how you're using the chain rule. It looks like you're simply using the product rule to obtain the derivative.

thecuriousether