filmov
tv
Find the Area of the Blue Triangle Inside of a Rectangle

Показать описание
In this video we use the formulas for the areas of rectangles and triangles, as well as the quadratic formula to find the area of the blue triangle.
Find the Area Challenge
Math Antics - Area
Finding the Area of a Composite Figure | Area of Composite Rectangles
How to Find the Area of a Rectangle | Math with Mr. J
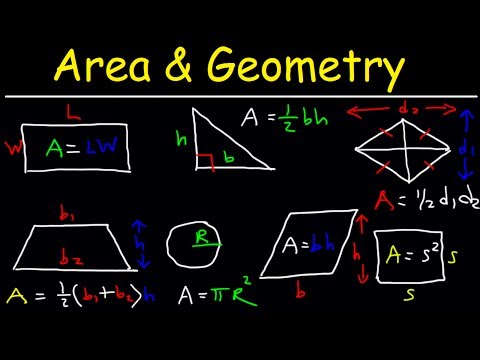
Area of a Rectangle, Triangle, Circle & Sector, Trapezoid, Square, Parallelogram, Rhombus, Geome...
Area for Kids
How to Find the Area of a Square | Math with Mr. J
How to Find Area | Rectangles, Squares, Triangles, & Circles | Math Mr. J
Find the area of triangle vertices are (1,2),(-3,4),(-5,-6) | Tnpsc gr 2 & 2a | Maths palace
Area and Perimeter
How to Find the Area of a Circle | Area of a Circle Step by Step
Can you find area of the Triangle? | (Simple Rule) |#math #maths | #geometry | #trigonometry
Finding the Area Between Two Curves by Integration
How to Find the Area of a Triangle | Calculate the Area of a Triangle
Area of a Trapezoid (Trapezium) | Math with Mr. J
How to Find the Area of a Circle | Math with Mr. J
Area of square | How to find area of the square #shorts
Can you find area of the Pink shaded region? | (Rectangle) | #math #maths | #geometry
(MATH) How to Find an Area of a Square? | #iQuestionPH
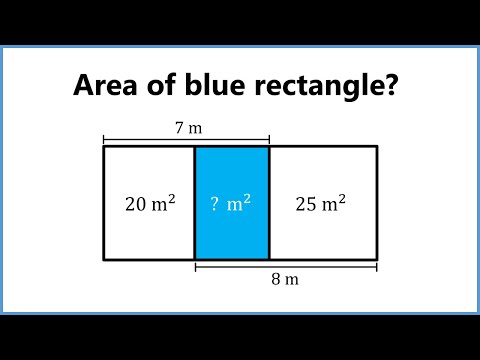
Find the area of the middle rectangle
Area of Parallelograms | How to Find the Area of a Parallelogram
How to Find the Area of a Circle Given the Diameter | Math with Mr. J
How to Find the Area of a Square or Rectangle
How to Find the Area of Rectangles and Squares | Math with Mr. J
Комментарии
 0:04:33
0:04:33
 0:10:26
0:10:26
 0:07:14
0:07:14
 0:04:43
0:04:43
 0:20:35
0:20:35
 0:08:58
0:08:58
 0:02:48
0:02:48
 0:22:10
0:22:10
 0:06:35
0:06:35
 0:17:49
0:17:49
 0:06:39
0:06:39
 0:08:41
0:08:41
 0:07:52
0:07:52
 0:06:37
0:06:37
 0:06:14
0:06:14
 0:09:08
0:09:08
 0:00:30
0:00:30
 0:09:53
0:09:53
 0:03:05
0:03:05
 0:03:25
0:03:25
 0:04:30
0:04:30
 0:05:28
0:05:28
 0:01:48
0:01:48
 0:06:57
0:06:57