What is a differential equation? Applications and examples.

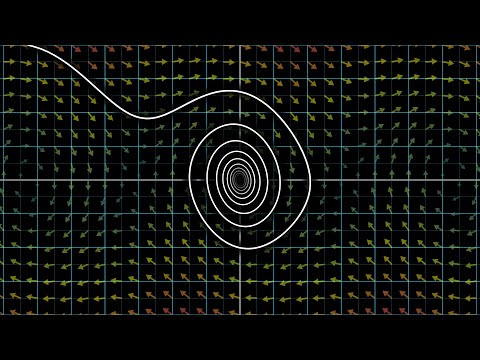
Learn what differential equations are, see examples of differential equations, and gain an understanding of why their applications are so diverse.

Specifically, watch to learn answers to the following questions.

1. What are some real-world applications of differential equations?
2. What is a differential equation?
3. Why might differential equations apply to so many real-world phenomena?
4. What are some examples of differential equations?

Additional Resources
To review the ideas in this video, try out the free "digital notecards" at the URL below.

I make one notecard for each video in the playlist. Each notecard contains a question or exercise that summarizes the content of the corresponding video.

The notecards can help you rapidly review what you've learned, especially if you haven't watched the videos in a while. You'll also find them helpful if you want to test your understanding right after you watch a video.

If you'd like to be notified when I post new videos in the playlist, just hit the subscribe button.

Happy learning!
Greg at Higher Math Notes

This video is part of a playlist:

[Googlu]

those who can explain in simple words surely know their stuff really well- thank you so much for this simple explanation! good luck

[ABC]

You just explained this thing so clearly that none of my so called Ph.d lecturers could do. Liked and now subscribed to your channel. Many thanks from India X

[solidus]

How does this channel not even have a thousand subscribers? What a shame, the videos are of high quality.

[sccm]

After you said all the applications of differential equations you made it look so much more interesting.

[crazyjester]

Any equation containing an unknown derivative is called differential equations.
Purpose solving for function not for a parameters (variable)

[hannananan]

Great job making this video! Really informative and easy to understand, thank you sir!

[braineedly]

Sir thanks for your explanation, it's very clear and concise

But I'm still not understand yet, how to determine differential equation?
like this:
y" + xy = e^2x

where did you get kind of equation like this sir?

I mean how do we determine equation in real life cases?

Thanks 🙏

[PankajKumarthinkvidya]

wow. Nice explanation. how do you make these video ..powerpoint ??

[yahyaasiri]

You made it very easy to understand and this is what we need.
Thank you so much

[natwoollard]

how do u solve the first equation u put

[asif.a]

Thank you so much, you made it look more easier👍

[gerardleon]

Is this the same with differential calculus in terms of real life application? ASAP PLS

[bmanjunatha]

thank your explanation is too good nailed it 😀

[robertbrandywine]

Excellent explanation. I would have added that the solution to a differential equation is a function.

[teentalex]

Can learning differentiation equations help with algebra

[sandilemasuku]

Hi, can you please explain the brain function or do an example of brain function please

[johnathanrendon]

This Vid did 50 textbook pages in 2 minutes and 10 seconds

[machonsote]

I think it would be better to start out by explaining how you arrive at a differential equation, instead of just writing out (what seems to be) meaningless equations that, right away, confuse those who are trying to learn.
Let me give you an example of how (I think) you should start:
"Before talking about how to deal with differential equations, let's look at how a simple differential equation is created".
Let us say that an "ant" scientist just bought an ant colony of 1000 ants to do an experiment. The experiment was to determine the rate at which the ants would die by introducing them to an ant "virus".
Turns out that each day, one-tenth of the remaining ant population died off.
The ant scientist came up with the following equation to represent the number of ants at any given day: y(t) = t is in "days"
At t=0 (right before the "virus" was introduced) y = 1000 ants
At t = 1 (1 day later) y = 900 (100 died off)
At t = 2 (2 days later) y = 810 (another 90 died of 900)
so on....
For the equation of y(t) = 1000e^(-0.10536t) : Taking the derivative (back from Calculus) of y with respect to t :
dy/dt = -105.36e^(-0.10536t) : This is the differential equation stating the rate of ants dying with respect to time (in days)
At t = 1, the rate is -95 (between -100, first day, and -90, second day)
At t = 2, the rate is -85 (between -90, second day and -80, third day)
....and so on....

After this, then you can explain that differential equations can get quite complex and then continue writing out differential equations.

[robinloyola]

Empezaste Bien BRO, despues la dañaste. Pilas con eso

[crazyjester]

Any equation containing an unknown derivative is called differential equations.
Purpose solving for function not a parameter (variable).