filmov
tv
Differentiating sin¯¹(x) & cos¯¹(x)

Показать описание
Differentiating sin¯¹(x) & cos¯¹(x)
Differentiating inverse trigonometric functions, cos–¹x,sin–¹x,tan–¹x
Write an algebraic expression for cos(sin^-1 x), cosine of inverse sine x
derivative of cos(sin^-1(x)), calculus 1 tutorial
Differentiate and sketch function cos inverse sine x
Prove that the derivative of cos^(-1) x= - 1/(sqrt(1-x^2)). Derivatives of Inverse Trig Functions
Derivative of cos(1/x) Trigonometric Functions
Derivative of inverse sine | Taking derivatives | Differential Calculus | Khan Academy
Does (-1)^x = cos(πx)? #maths #calculus #eulerstheorem
Find derivative of y = cos^(-1) (1/x) with respect to x. Inverse Trig Functions
Prove cos inverse derivation formula Trig Calculus
Differentiation - sin(x) and cos(x)
Find dy/dx if y = cos⁻¹(1-x²/1+x²), x∈(0,1) Ncert problems differentiation inverse trigonometry...
Class 12th – Prove Sin Inverse X+Cos Inverse X = Pie/2 | Trigonometric Function | Tutorials Point
Derivative of `sin^(-1)x` w.r.t. `cos^(-1) sqrt(1-x^(2))` is -
Derivative of Sine and Cosine Functions | Calculus
If ` y = sin^(-1) (cos x) ` , then derivative of y is
Differentiate y = (1 + sin(x))/(x + cos(x))
Differentiating sin(x), cos(x) and tan(x)
If y=cos⁻⁻¹x, find d²y/dx² in terms of y alone ,second order Ncert continuity and Differentiation...
Differentiation of cos inverse x | differentiation of cos^-1 x | derivative of cos inverse x
Prove that cos(sin^(-1)) = sqrt(1-x^2). Inverse Trig Functions
How to calculate inverse cos in scientific calculator #scintific #calculator #studenthacks
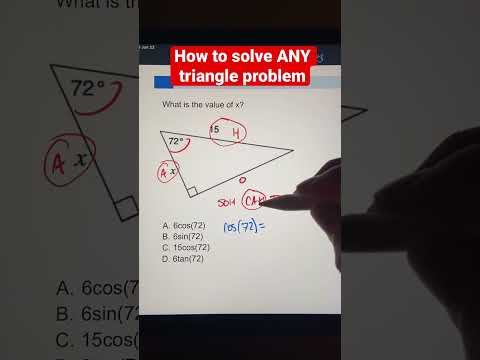
Missing Side of a Triangle Trigonometry Problem SOH CAH TOA (sin, cos, tan) #shorts #maths #math
Комментарии
 0:16:13
0:16:13
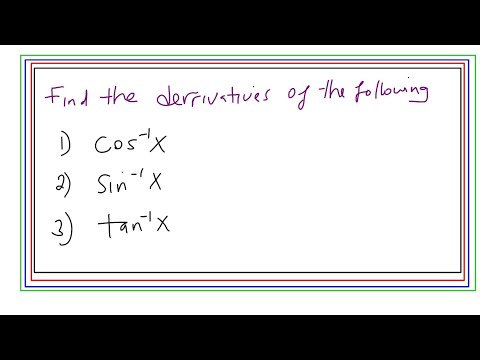 0:09:49
0:09:49
 0:03:28
0:03:28
 0:01:08
0:01:08
 0:07:52
0:07:52
 0:03:19
0:03:19
 0:05:11
0:05:11
 0:04:56
0:04:56
 0:02:04
0:02:04
 0:04:01
0:04:01
 0:04:08
0:04:08
 0:05:35
0:05:35
 0:01:59
0:01:59
 0:04:58
0:04:58
 0:03:35
0:03:35
 0:10:31
0:10:31
 0:02:01
0:02:01
 0:02:38
0:02:38
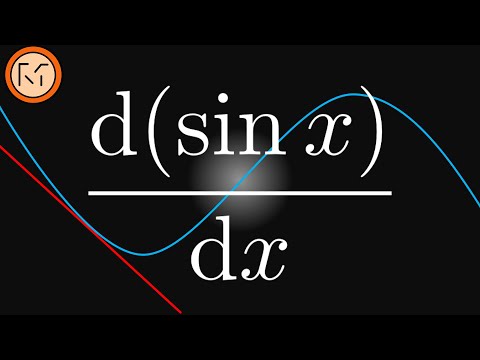 0:07:30
0:07:30
 0:03:28
0:03:28
 0:02:25
0:02:25
 0:02:30
0:02:30
 0:00:15
0:00:15
 0:00:39
0:00:39