filmov
tv
Russian Math Olympiad Problem | A Very Nice Geometry Challenge | 2 Different Methods

Показать описание
Russian Math Olympiad Problem | A Very Nice Geometry Challenge | 2 Different Methods
MY OTHER CHANNELS
••••••••••••••••••••••••••••••••
--------------------------------------------------------------------------------
Join the channel to become a member
MY OTHER CHANNELS
••••••••••••••••••••••••••••••••
--------------------------------------------------------------------------------
Join the channel to become a member
Russian Math Olympiad Question
Russian Math Olympiad | A Very Nice Geometry Problem
Russia | Math Olympiad Question | You should know this trick!!
Russian Math Olympiad Problem | A Very Nice Geometry Challenge | 2 Different Methods
Russian Math Olympiad Problem | A Very Nice Geometry Challenge
Find all integer solutions (Russian Math Olympiad)
Russian Math Olympiad Question || Find the value of X ||
Solving a Russian Math Olympiad Problem | Solve for x If 4^27 + 4^1000 + 4^x is a Perfect Square
Poland | Math Square Root Problem | Math Olympiad
Russian Math Olympiad Problem | A Very Nice Geometry Challenge | 2 Different Methods
The Man Who Solved the $1 Million Math Problem...Then Disappeared
Russian | Math Olympiad | A Very Nice Algebra Problem 😊| Find the value of X & Y=??
Russian Math Olympiad | Best Geometry Problems
Russian -Math Olympiad|Solve for x and y#math #matholympiad
Russian Math Olympiad Geometry Problem | Best Math Olympiad Problems | 2 Different Methods To Solve
Russian Math Olympiad Question.Japanese | Can you solve this ? | Math Olympiad
Russian Math Olympiad | A Very Nice Geometry Problem | 2 Different Methods
Russian- Math Olympiad Question International Maths Olympiad Problem | Find Value of X
How to solve this Russian Olympiad Math Questions | Learn the trick to solve this Math Problem
Russian Math Olympiad Question | How to solve this
Can you solve this Russian - Math Olympiad Question ??#maths #mamtamaam
Russian Math Olympiad Question #radicalexpression#mathcontest
Russian - Math Olympiad Question | Find Limit of Function ❓
Russian Math | Junior Math Olympiad Question | Square root problems.
Комментарии
 0:03:42
0:03:42
 0:14:34
0:14:34
 0:08:01
0:08:01
 0:27:41
0:27:41
 0:14:34
0:14:34
 0:20:56
0:20:56
 0:03:42
0:03:42
 0:07:27
0:07:27
 0:08:04
0:08:04
 0:17:48
0:17:48
 0:10:45
0:10:45
 0:08:33
0:08:33
 0:09:58
0:09:58
 0:10:40
0:10:40
 0:24:49
0:24:49
 0:03:29
0:03:29
 0:19:49
0:19:49
 0:04:31
0:04:31
 0:09:35
0:09:35
 0:02:12
0:02:12
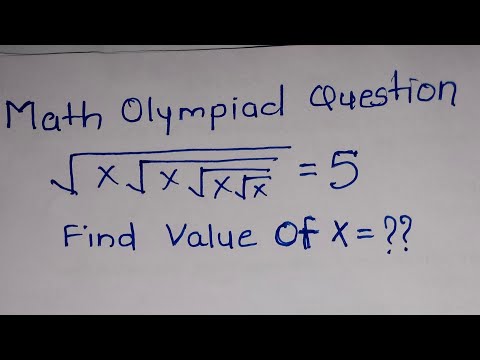 0:03:14
0:03:14
 0:04:20
0:04:20
 0:05:35
0:05:35
 0:03:32
0:03:32