Poisson's Ratio, Axial Strain, and Transverse Strain Problem and Solution (Strength of Materials)

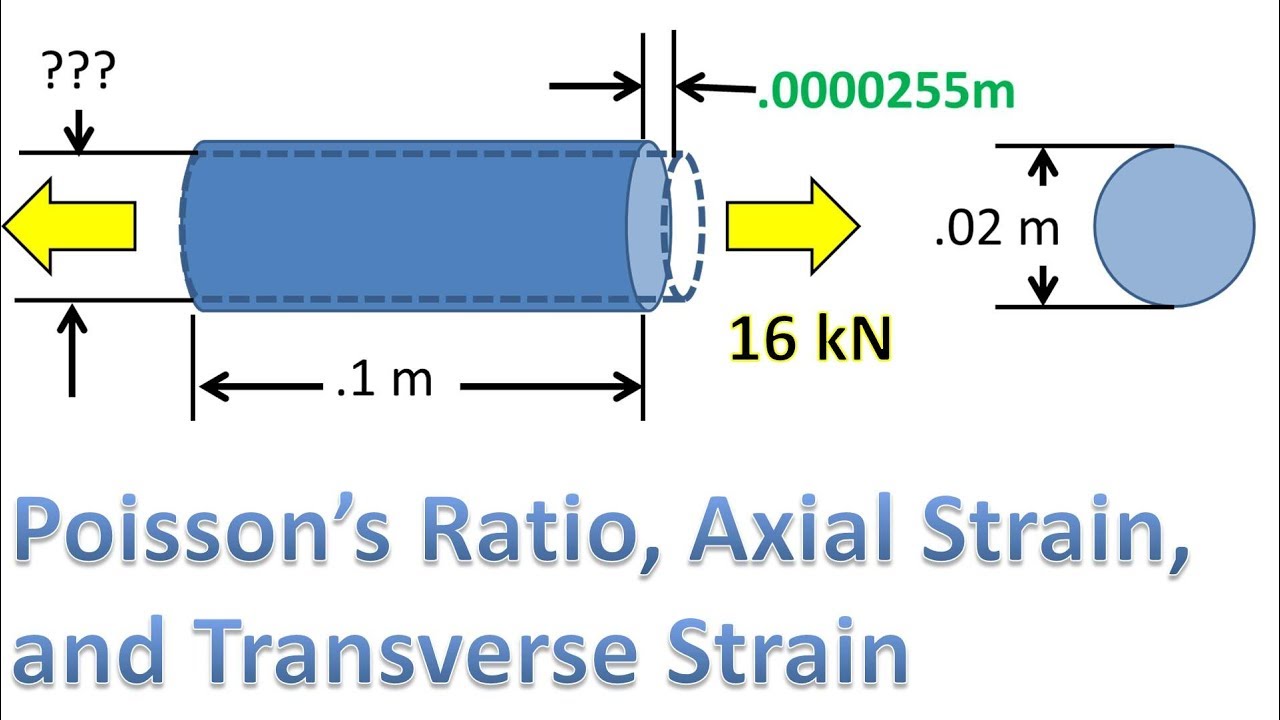
In this problem we have a cylindrical steel rod with diameter of .02 m and length of .1m (with no force acting on it) It has a load applied in tension of 16 kilo newtons. Find the change in diameter given a poison ratio of the material of .29 which the poisson ratio will be abbreviated as greek leter mu.
We previously completed the deformation portion of the rod in the axial direction in the video “object under tension find change in length” video and got a axial deformation of .0255 milimeters. We also found that it was within the proportional limit so hookes lawes applied and the poisson ratio also applies.
To better understand what the poisson ratio is. We must first understand what strain is. Strain is the ratio of the deformation of an object over its original length.
So in the transverse direction or in other words the direction that is perpendicular to force applied. We have that the transverse strain equals the total deformation across the diameter over the orginal diameter.
In the axial direction we have that the deformation in the length of the rod over the orginal length equals the axial strain.
So if we divide the transverse strain over the axial strain we get the Poissons ratio. The poisson ratio is the ratio that compares how much the part will expand or contract in the transverse direction versus the axial direction. So if we have the axial strain and poison ration we can find the transverse strain. And if we have the tranverse strain and poison ration we can find the axial strain.
Now its useful to note that in tension the diameter will decrease while the length with increase. So the tranverse strain is negative while the axial strain is possive.
On the other hand under compression the diameter will increase and the length will decrease. So the tranverse strain is positive while the axial strain is negative.
In our example we are under tension so the tranverse strain will be negative and the axial strain will be positive. So the part will increase in length but decrease in diameter.
Going back to our problem if we take the axial deformation over the length of the rod of .1m we get an axial strain of .000255. Note this is unitless because we are dividing length by length.
We can plug our axial strain into the possons ratio formula.
To get the transverse strain to one side of the equation we can multiply both sides by the axial strain
We end up with a transverse strain of .00007395
Now we can set what we found transverse strain to be equal to and set it equal to the deformation over the diameter of the rod. which the deformation is the total deformation of the diameter over the initial diameter of .2 m
We get a total deformation of .000001479
With that knowledge we can take the total deformation of the diameter and add it to the intial diameter to get the final diameter. We get a final diameter of .019998521 meters.
For your reference I have listed out all of the step in algebra form.

Disclaimer
These videos are intended for educational purposes only (students trying to pass a class) If you design or build something based off of these videos you do so at your own risk. I am not a professional engineer and this should not be considered engineering advice. Consult an engineer if you feel you may put someone at risk.

[VAM_Physics_and_Engineering]

One small error a negative sign is outside of parentheses should be (poissons ratio) multiplied times (-axial deformation/length) on the slide that goes over compression strain and poisons ratio