filmov
tv
REAL rotations within IMAGINARY numbers! #shorts

Показать описание
#shorts #short #comboclass #imaginary #imaginarynumber #imaginarynumbers #number #numbers #negative #positive #math #maths #mathematics
Combo Class is a crazy educational show where you can have fun learning rare things about math, science, language, and more! This is the SHORTS channel for faster-paced videos. Make sure you're also subscribed to the main Combo Class channel where full episodes go!
DISCLAIMER: any use of fire, tools, or other science experiments in this series is always done in a safe and professional way. Do not try to copy any actions you see in this series yourself.
Combo Class is a crazy educational show where you can have fun learning rare things about math, science, language, and more! This is the SHORTS channel for faster-paced videos. Make sure you're also subscribed to the main Combo Class channel where full episodes go!
DISCLAIMER: any use of fire, tools, or other science experiments in this series is always done in a safe and professional way. Do not try to copy any actions you see in this series yourself.
REAL rotations within IMAGINARY numbers! #shorts
Why Complex Multiplication Produces Rotation
Imaginary Numbers Are Real [Part 1: Introduction]
How Imaginary Numbers Were Invented
Imaginary Numbers Are Just Regular Numbers
The Real World Uses of Imaginary Numbers
Where do Imaginary Numbers come from?
e^(iπ) in 3.14 minutes, using dynamics | DE5
Imaginary Numbers Explained Bob Ross Style
Imaginary Number Pattern
Rotational illustration of imaginary numbers versus real number line
Complex rotation
What is a Complex Number
Why 'imaginary numbers' have such a bad name... #shorts
Imaginary numbers aren't imaginary
Complex Numbers 3D #math #animation #complex #numbers #learn #study
Necessity of complex numbers
ARE IMAGINARY NUMBERS APPLICABLE IN REAL LIFE TOO ?
Imaginary numbers finally shown REAL in daily life
Complex number fundamentals | Ep. 3 Lockdown live math
Understanding Imaginary Numbers | BetterExplained
What's the physical meaning of imaginary numbers?
Imaginary Numbers, Exponents and One #Shorts
Imaginary Numbers are Not 'Imaginary'! In 5 Levels of Complexity
Комментарии
 0:00:58
0:00:58
 0:05:44
0:05:44
 0:05:47
0:05:47
 0:23:29
0:23:29
 0:09:02
0:09:02
 0:16:49
0:16:49
 0:01:00
0:01:00
 0:04:08
0:04:08
 0:11:23
0:11:23
 0:00:59
0:00:59
 0:05:42
0:05:42
 0:06:20
0:06:20
 0:01:00
0:01:00
 0:00:58
0:00:58
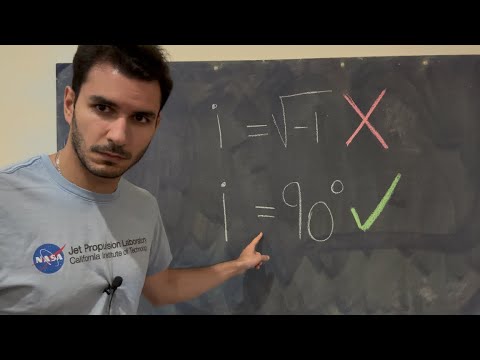 0:13:55
0:13:55
 0:00:22
0:00:22
 0:07:39
0:07:39
 0:08:24
0:08:24
 0:32:27
0:32:27
 1:22:11
1:22:11
 0:14:23
0:14:23
 0:06:03
0:06:03
 0:00:59
0:00:59
 0:13:59
0:13:59