filmov
tv
Vector Fields - Calculating the Line Integral Work Around Closed Paths
Показать описание
This is part of my classical mechanics series. You can find all my videos in the series in the following playlist.
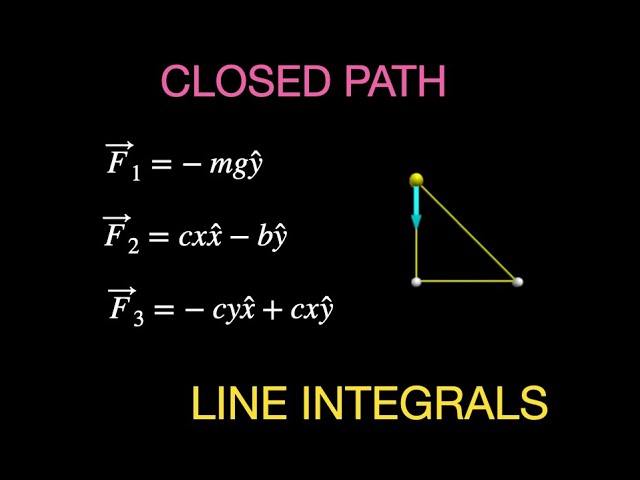
Here are three vector fields:
F1 = -mg y-hat
F2 =cx x-hat - b y-hat
F3 = -cy x-hat + cx x-hat
For each field, I calculate the work around a closed path - both analytically and numerically (with python).
Here is the code
Here are three vector fields:
F1 = -mg y-hat
F2 =cx x-hat - b y-hat
F3 = -cy x-hat + cx x-hat
For each field, I calculate the work around a closed path - both analytically and numerically (with python).
Here is the code
Vector Fields, Divergence, and Curl
Divergence and curl: The language of Maxwell's equations, fluid flow, and more
Conservative Vector Fields // Vector Calculus
Vectors, Vector Fields, and Gradients | Multivariable Calculus
Intro to VECTOR FIELDS // Sketching by hand & with computers
Finding the scalar potential function for a conservative vector field // Vector Calculus
Introduction to Vector Fields
The Gradient Vector Field
Vector Calculas | gradient | Engineering mathematics
Calculus 3 Lecture 15.1: INTRODUCTION to Vector Fields (and what makes them Conservative)
Scalar and vector fields | Lecture 11 | Vector Calculus for Engineers
The Divergence of a Vector Field: Sources and Sinks
Fluid flow and vector fields | Multivariable calculus | Khan Academy
Line integrals and vector fields | Multivariable Calculus | Khan Academy
How to Evaluate the Line Integral of a Vector Field
Line Integrals of Vector Fields // Big Idea, Definition & Formula
Electric Field Vector Formula With R-Hat Vector and Position Vector - College Physics
Vector Calculus Complete Animated Course for DUMMIES
Example of sketching a vector field.
Div, Grad, and Curl: Vector Calculus Building Blocks for PDEs [Divergence, Gradient, and Curl]
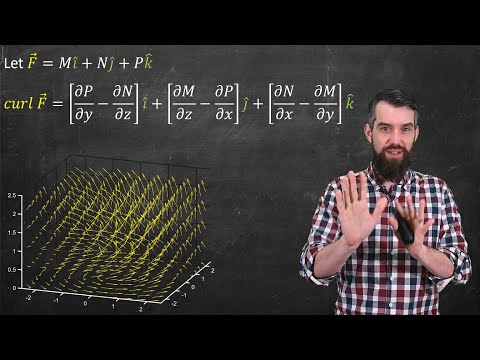
The CURL of a 3D vector field // Vector Calculus
Vector Fields (Introduction)
Finding a Potential for a Conservative Vector Field
Divergence and Curl (Vector Fields)
Комментарии
 0:15:36
0:15:36
 0:15:42
0:15:42
 0:06:17
0:06:17
 0:20:26
0:20:26
 0:12:09
0:12:09
 0:12:06
0:12:06
 0:11:30
0:11:30
 0:02:18
0:02:18
 0:24:15
0:24:15
 0:58:14
0:58:14
 0:08:53
0:08:53
 0:20:57
0:20:57
 0:03:35
0:03:35
 0:16:47
0:16:47
 0:06:16
0:06:16
 0:08:40
0:08:40
 0:21:38
0:21:38
 0:46:44
0:46:44
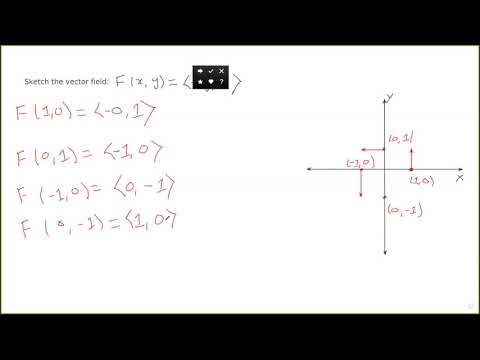 0:06:44
0:06:44
 0:13:02
0:13:02
 0:08:26
0:08:26
 0:10:20
0:10:20
 0:10:07
0:10:07
 0:13:11
0:13:11