Find the VELOCITY Of A Pendulum at It's Lowest Point

I am not sponsored by Sharpie... yet.

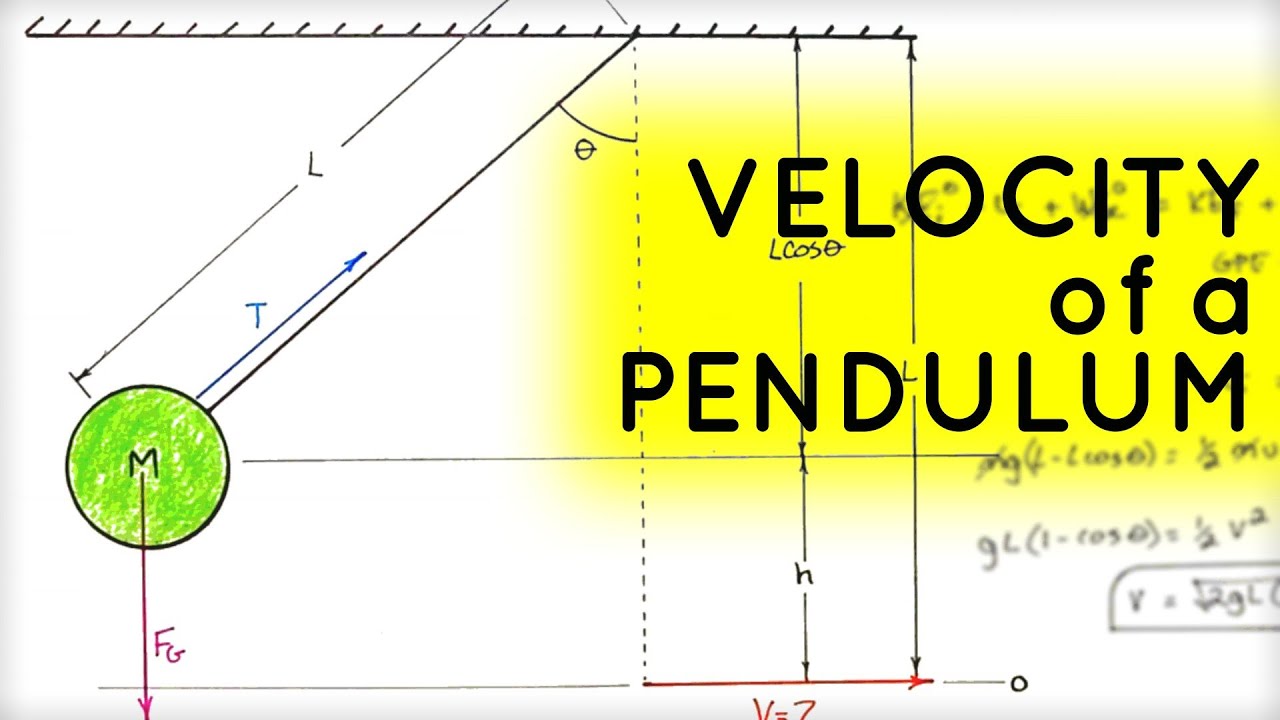
A common application of the work energy theorem, this problem looks at the conservation of energy as gravitational potential energy is converted into kinetic energy through work by gravity.

The mass begins with some potential energy relative to its lowest point. But as the pendulum is released gravity does work on the pendulum to convert potential energy into kinetic energy.

At any point, if you can find how much potential energy has been lost, then you can solve for the kinetic energy and there for solve for the velocity of the pendulum.

Just for fun, If you try to solve for the velocity of the pendulum at a point higher than the release height, you will get an imaginary number. In mechanics the result of an imaginary number means it cant happen... That is to say the ball can not go higher than that from which it was released.

This problem commonly comes up in physics including AP Physics 1 and AP Physics C

[ptyptypty]

don't ever stop making your videos !! they are very educational and ENTERTAINING. Your attention to detail and presentation are Unique. Thank you. By the way, I've seen lots of videos on this Problem, that is, WHAT is the velocity at the Bottom... but I could NEVER Find a video that gave the equation for finding the Velocity of the Bob at any point after it was released. I had to figure that out on my own.. lol.. and that's that.

[Homie-world]

I have a question please help,
we know when object comes downward PE will be -Mgh but you took +Mgh.
Why?

[iridianramos]

Hi! I have a question. I'm doing an experiment based on this showing how the moment of inertia changes based on different distributions of mass. This relationship can be demonstrated by shortening the string length of a simple pendulum and measuring the velocity at the bottom of its swing for each string length. However, I'm confused on why my experimental velocities are all different from each other. I was told this would work by my physics teacher, but I'm confused. If the height to which I'm raising the pendulum doesn't change for each string length and therefore, neither does the potential energy then neither should the kinetic energy for each new string length. But all of my velocities are different. I know the angular velocity should be different but I'm finding the time taken to swing at the bottom of the pendulum (then used to find the velocity and then the angular velocity) changes when it shouldn't. Essentially, experimentally the velocity at the bottom of its swing changes between different string lengths indicating changes in angular velocities but theoretically, the velocity shouldn't change and only the angular velocity should. What is the theory behind these theoretical and experimental differences?

[trulluyt]

Let's say that at the release point, it is moving with some initial tangential velocity. So then you can calculate the total energy of the system by calculating the KE at that point and the PE. Now, we can convert all that to PE and find maximum height, and therefore angular displacement. Using that angular displacement, you can have the function: You differentiate the function and you take the coefficient as the maximum angular velocity. You multiply that with the length of the string to calculate linear velocity. This linear velocity will, for some reason, be different from the normal energy conservation method. Why does this happen? I genuinely don't know.

[Alphamatics]

Do we have to rake the centre of gravity

[endritduraku.G]

what about the velocity in a specific position?