filmov
tv
Finding the distance from a point to a line (using vectors)

Показать описание
----------------------------------------
Big thanks to my Patrons for the full-marathon support!
Ben D, Grant S, Mark M, Phillippe S. Michael Z, Camille E.
Nolan C. Jan P. Devun C. Stefan C. Budoray Ethan BW
----------------------------------------
#blackpenredpen #math #calculus #apcalculus
How to Find the Distance Between Two Points - How to Use the Distance Formula
How To Find The Distance Between Two Points
How To Find The Distance Between a Point and a Plane
Finding Distance from a Point to a Line
Applying the distance formula to find the distance between two points
The Distance Formula: Finding the Distance Between Two Points
Rule of Thumb - Distance ( EASY !!! ). No Math Needed
Distance Between Point and Plane - Example 1
Unlocking the Secrets: How to Calculate Actual Distance Like a Pro!
Find the distance and midpoint between two points
A-Level Further Maths F5-07 Intersections: Finding the Distance from a Point to a Plane
Distance between a point and a line | Analytic geometry | Geometry | Khan Academy
Finding Distance from Point to Line (Formula)
Distance Formula
Distance between a point and a line (vectors) (KristaKingMath)
Find Distance Between a Point and a Line in 3D
How to Find the Distance Between Two Points - The distance formula made easy!
Example finding distance with Pythagorean theorem
Finding Distance using the Pythagorean theorem
Using Distance Formula to Find Distance Between Two Points!
Find the distance between the points (-2,0) and (4,5)
Determining the Distance Between a Line and a Point
Shortest Distance of a Point from a Line
Determining the Distance Between a Plane and a Point
Комментарии
 0:04:36
0:04:36
 0:05:19
0:05:19
 0:10:47
0:10:47
 0:03:35
0:03:35
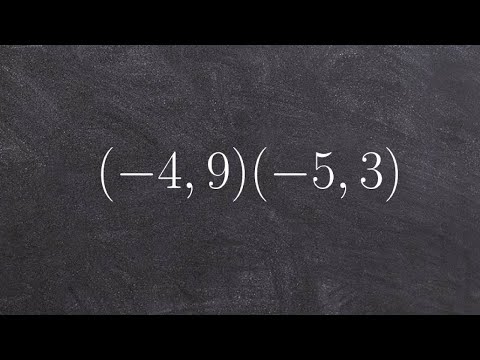 0:04:21
0:04:21
 0:03:38
0:03:38
 0:04:27
0:04:27
 0:04:34
0:04:34
 0:26:53
0:26:53
 0:03:01
0:03:01
 0:06:36
0:06:36
 0:05:32
0:05:32
 0:02:43
0:02:43
 0:06:32
0:06:32
 0:08:52
0:08:52
 0:14:22
0:14:22
 0:05:25
0:05:25
 0:03:40
0:03:40
 0:02:55
0:02:55
 0:05:21
0:05:21
 0:03:03
0:03:03
 0:08:35
0:08:35
 0:09:57
0:09:57
 0:05:18
0:05:18