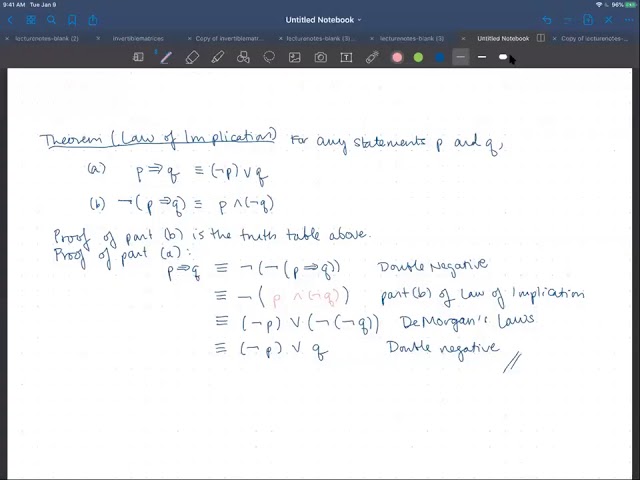
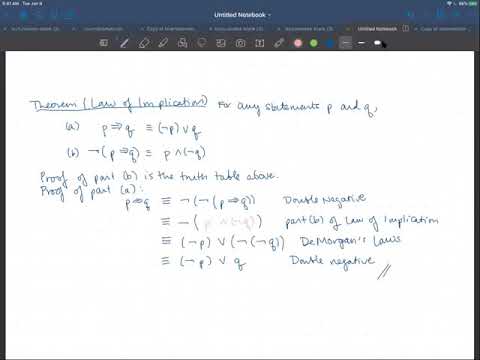
Implication and Biconditional Statements

The definition of implication and biconditional connectives along with some laws for working with them, plus the definition of tautology and contradiction.

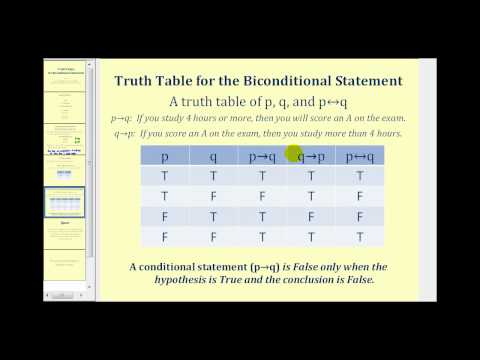
(In the part I got hung up on in the video, "p is necessary for q" can be read "p if q" (or "if q, then p"), and "p is sufficient for q" can be read "p only if q" (or "if p then q"). So, "p is necessary and sufficient for q" literally translates to "p if and only if q.")