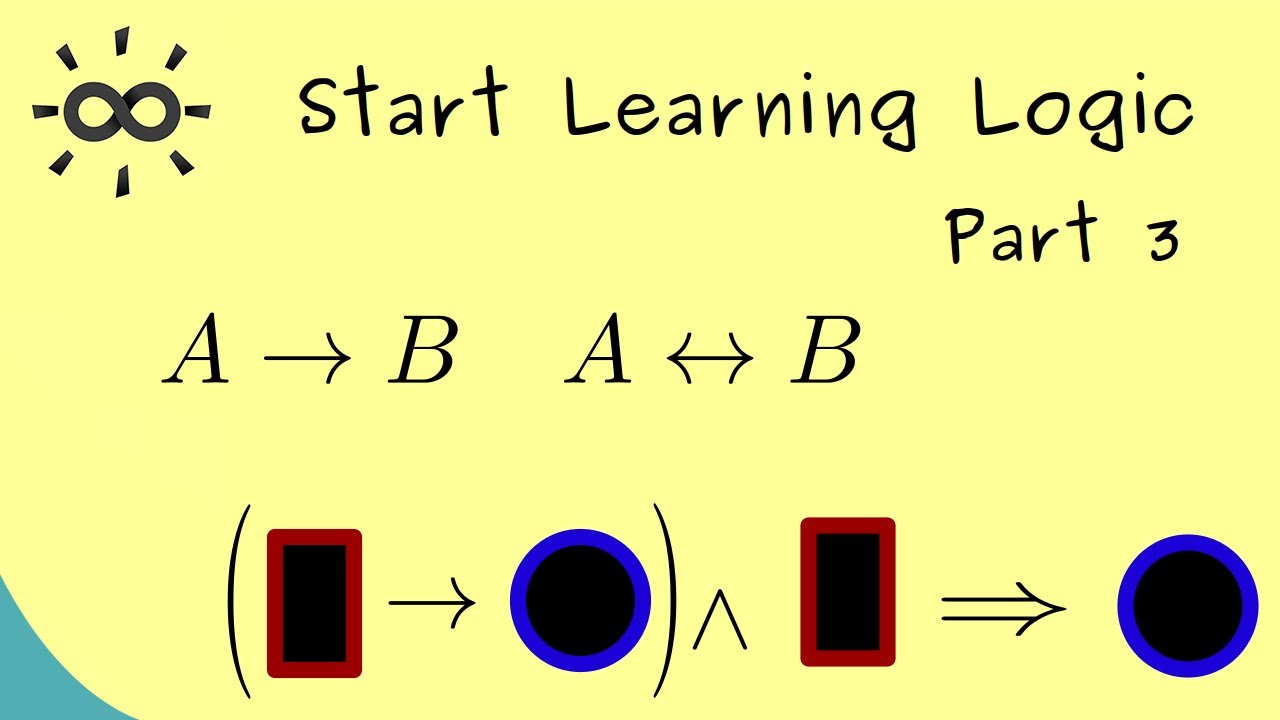
Start Learning Logic 3 | Conditional, Biconditional, Implication and Deduction Rules

Thanks to all supporters! They are mentioned in the credits of the video :)

This is my video series about Start Learning Logic. I hope that it will help everyone who wants to learn about it.

#StartLearningMathematics
#Mathematics
#LearnMath
#Calculus
#Logic

x

I hope that this helps students, pupils and others. Have fun!

(This explanation fits to lectures for students in their first and second year of study: Mathematics for physicists, Mathematics for the natural science, Mathematics for engineers and so on)

[punditgi]

So rare for a teacher to explain the difference between the material conditional and an implication, the latter of which is indeed a tautology. This is just one example among many as to why your lessons stand above most others. Bravo, sir! 😃

[StankyPickle]

The explanation of reductio ad absurdum using conditionals makes so much sense! I struggled to understand why it worked for so long, and accepted it as a thing I had to memorize. This video made it suddenly click for me. Thank you!

[theoendre]

Thank you very much for the great content, you are a life saver.

[ya-hengyang]

Thanks！ From Wikipedia, reductio ad absurdum is Latin for "reduction to absurdity".

[JoannBaron]

Why doesnt this guy have 10 millions subscribers seriously???

[jackgreen]

1:44
double arrow means, that standard arrow (conditional) gives tautology
For some kind of reason it doesn't make sense for me without "that"

[oskaradolfson]

Please continue when possible this series! :D

[jungakira]

How about thinking Reductio ad absurdum in this way?
Reductio ad absurdam: (A->B) <=> (A ^~B -> 0)
example: we want to prove "Square root of 2 is not a rational number". In "(square root of 2) ^ (rational)" we can find that it is false. so the first statement is true.

[EdmundAmonoo]

Your teachings are good
But I think there's a mistake in conditional side where you were trying to prove that A ^ B =>B
The third one on the table. If I'm wrong please let me know

[Dupamine]

At 1:05, why can we 'follow everything' if we start from false? What does that mean? Why is everything true when A is false? I still dont get it

[sportmaster]

Thanks for the videos Sir! Do you think they are good to watch to prepare for studying maths at university in the UK ?

[duyguolpak]

Are there any videos on your Steady platform that are not on YouTube?

[b.kpiano]

I am forced to subscribe for your channel because of content and your teaching style.