filmov
tv
Mean and Variance of OLS Estimators in Matrix Form Linear Regression

Показать описание
This video follows from the previous one covering the assumptions of the Linear Regression Model in the Matrix Formulation to derive and show the properties of the OLS estimators, E[B] and Var[B].
In this video I derive and show that under the assumptions of the Linear Regression Model, the OLS Estimators are unbiased (E[B] = B) and that the Variance of B (Var(B) = sigma squared*(X'X)^-1).
#Econometrics
#Regression
#OLS
0:00 Introduction
0:16 Derive and show that E[β^] = β
3:05 Derive Var[β^]
In this video I derive and show that under the assumptions of the Linear Regression Model, the OLS Estimators are unbiased (E[B] = B) and that the Variance of B (Var(B) = sigma squared*(X'X)^-1).
#Econometrics
#Regression
#OLS
0:00 Introduction
0:16 Derive and show that E[β^] = β
3:05 Derive Var[β^]
Deriving the mean and variance of the least squares slope estimator in simple linear regression
Mean and Variance of OLS Estimators in Matrix Form Linear Regression
Variance of the OLS estimator (Part 1)
Variance of OLS estimators - part one
Variance of OLS estimators | Linear Regression Model | Econometrics | Harpreet Kaur | Ecoholics
Variance and Standard Error of OLS Estimates | Introductory Econometrics 11
(Un)Conditional mean and variance of the OLS beta estimate || Econometrics || U/Grad || MPhil || PhD
ECO375F - 2.6 - Variance of the Slope Estimator (β1)
Basic Econometrics - The variance of the OLS estimator
The variance of the OLS estimators
3.4 Variance of OLS estimators
Variance of Least Squares Estimators - Matrix Form
3.17 - The Variance of OLS Estimators
Estimated variance of OLS estimators - intuition behind maths
Estimating the variance of the OLS estimators
Find the Value of OLS estimators Linear Regression Model | Mathematical Economics | Ecoholics
Econometrics 31: Mean and Variance of OLS Estimators.
Least Square Estimators - Variance of Estimators, b0 and b1, Proof
10.3) OLS: Variance
Variance of OLS Intercept
ECO375F - 1.0 - Derivation of the OLS Estimator
Deriving the least squares estimators of the slope and intercept (simple linear regression)
Introduction to residuals and least squares regression
2.5b1 Variances of OLS estimators Part 1
Комментарии
 0:10:54
0:10:54
 0:08:38
0:08:38
 0:02:16
0:02:16
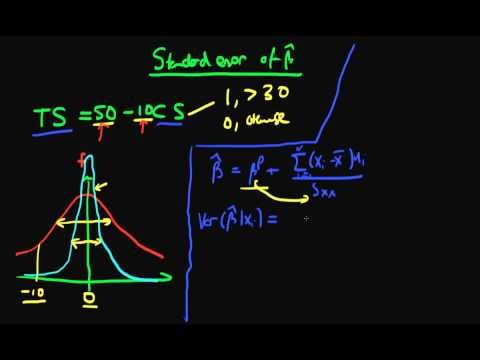 0:07:10
0:07:10
 0:06:17
0:06:17
 0:17:18
0:17:18
 0:09:55
0:09:55
 0:06:56
0:06:56
 0:17:39
0:17:39
 0:14:03
0:14:03
 0:17:08
0:17:08
 0:05:32
0:05:32
 0:03:35
0:03:35
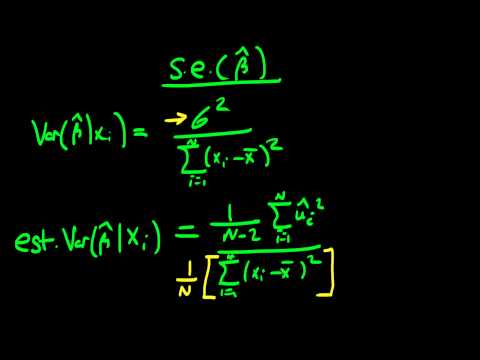 0:03:52
0:03:52
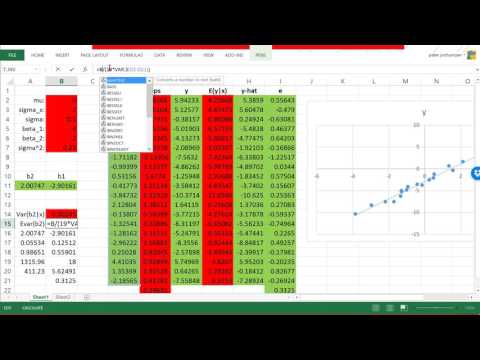 0:09:40
0:09:40
 0:08:56
0:08:56
 0:39:09
0:39:09
 0:30:11
0:30:11
 0:03:48
0:03:48
 0:06:52
0:06:52
 0:32:03
0:32:03
 0:12:13
0:12:13
 0:07:39
0:07:39
 0:12:16
0:12:16