How to solve PDE via method of characteristics

Показать описание

Рекомендации по теме

Комментарии

I DO NOT really have time to write this review, but I have to take time to thank you Dr Chris. I do have an exam tomorrow and i have no single idea of whats going on in my pde class, i dont think i can pass the exam until I saw your video, I think I can just ace the exam very easily. Thank you so much Dr Chris, you have saved thousands of students life.Hopefully that I can see your more videos.

thomasyang

I love math. I will watch these videos when I'm done watching the ODE videos. Thanks for these videos.

dolphinsatsunset

Thank you so much! Your video clarified the solution step by step and explained all the methods that were used. It helped me to get a better understanding of the material. Thank you again.

ekaterinakruglov

Yes, this is an interesting generalization. You can find the method for that problem in my PDE playlist.

DrChrisTisdell

For those who do not understand why (x, y)(b, -a) = k, you can easily think of it like this: the equation of a line is given by: m *x* + n *y* + c = 0 where (-n, m) is a *direction vector*, in our case: the direction vector is (a, b) so: n = -a and m = b hence the equation of that line is: b *x* -a *y* + c = 0 or b *x* -a *y* = k where k = -c

SO-dlpv

I understand the concept not just the procedure....thanks Chris

B.A.Gondal

This is something that I plan to do later this year when I teach a full course on PDE.

DrChrisTisdell

Hi Dr.Chris, If possible can you tell why the points on u=constant satisfy the equation bx-ay=k?

srinivaskandula

Thank you so much! This cleared up a lot of issues I was having.

nenny

Here are things that initially confused me and later found answer to:
1. For directional derivative to be zero, you can be travelling perpendicular to the gradient too. Why then has Dr. Chris taken only the constant u case?
Well, both are one and the same. Gradient is the direction of steepest ascent. Let's assume you are in a point on the mountain and looking towards the steepest line is the gradient. Keep your body fixed, but rotate your head around. You will eventually go from looking up at the steep to down the slope. You will pass through a line that has no slope. And that line is going to have constant u. Also, that line would be perpendicular. Consider this (a, b).(x, y) has some value (considering both are non zero) except for at 90 degrees.
2. Why (x, y).(-b, a)?
The equation of a line in cartesian form along (a, b) through (x0, y0) is (x-x0)/a=(y-y0)/b. On solving you get b(x-x0)=a(y-y0). Put b(x0)-(a(y0) as a constant. You can see where that comes from

potato

What if the characteristic lines are not straight lines but some curves?
Oh, and does this technique also work for higher-order equations? I think it should, because I know that at least the wave equation can be solved with characteristics. So how can this concept be generalized for higher-order equations? I can't quite see how gradients/directional derivatives apply there...

bonbonpony

The right hand side of the PDE is zero. The left hand side of the PDE is a special dot product. Since we have a PDE the left hand and right hand sides must be equal.

DrChrisTisdell

Thank you so much professor!
would be great if you could clear my confusion about Linear PDE: solution of a linear pde can always be represented by a linear combination, is it true?

helalme

I have a question what if a and b are variables of x and y not constants? if anyone has an answer to this that would be great because my course has only shown us how to do questions with a and b being constant

zanahaze

Can someone please explain why is he using normal vector (to the line) when he is searching for characteristics

antejurcevic

Where is this general solution? Can't find it.

Thank you for all your work!

amundjenssen

8:00 : doesn't the constant K have to be zero for the vectors to be normal to each other?

ThomasHaberkorn

Hello,
Your are a great professor. I'm learning a lot with your youtube channel.
Does exists a PDF for this serie of lesson (on the PDE).
Thanks a lot
Eric

ericrosenkrantz

how is the dot product 0 ... please explain

adityamorey

thanks alot sir.. very helpful.. do make more vids..

sophomore grad IIT kanpur, India

adityamorey

How to solve PDE via method of characteristics

How to solve PDE via change of variables

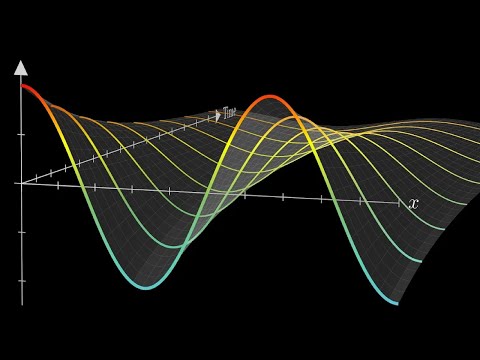
But what is a partial differential equation? | DE2

How to solve PDE via change of co-ordinates

Example of how to solve PDE via change of variables

Solve PDE via an integrating factor

How to solve PDE via method of characteristics

Solving a PDE using the integrating factor method

Solving the heat equation | DE3

'Introduction to Modern Scientific Programming and Numerical Methods' summary by author

Solving PDE using Separation of Variables Method

Method of Characteristics: How to solve PDE

PDE 5 | Method of characteristics

PDE: Heat Equation - Separation of Variables

SOLUTION OF FIRST-ORDER HOMOGENEOUS PDE(CHANGE OF COORDINATES METHOD)

PDE 101: Separation of Variables! ...or how I learned to stop worrying and solve Laplace's equa...

Solve the Partial Differential (PDE) 3Ux +5Uy =0 by the method of characteristics. (University Math)

Nonlinear PDE of order one: Standard form 4: Method of solution and Problems. Lect. # 10.

PDE 13 | Wave equation: separation of variables

Partial Differential Equations Overview

Solving Heat equation PDE using Explicit method in Python

How to solve any PDE using finite difference method

Solving the Heat Equation with the Fourier Transform

Solving the 2D Laplace PDE using Separation of Variables

Partial Differential Equation Lesson 2 ( Solutions to First Order PDE I )