filmov
tv
Calculus 1 -- Concavity; second derivative test -- More practice

Показать описание
0:00 Introduction
0:39 Problem 1
8:38 Problem 2
19:47 Problem 3
32:32 Problem 4
38:53 Problem 5
48:24 Problem 6
58:33 Problem 7
1:09:55 Problem 8
1:17:20 Problem 9
1:28:27 Problem 10
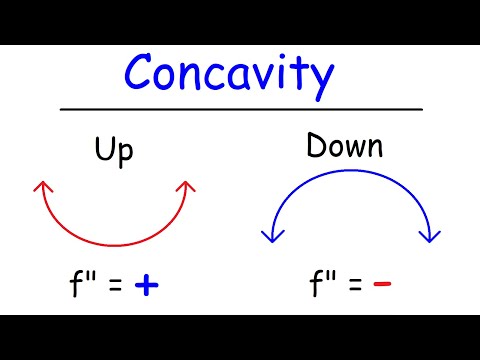
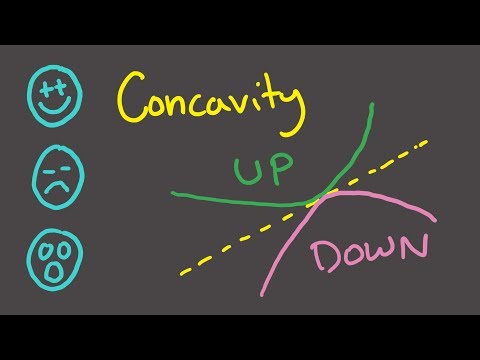
Concavity, Inflection Points, and Second Derivative
Calculus 1 Lecture 3.4: The Second Derivative Test for Concavity of Functions
Calculus 1 -- Concavity; second derivative test -- More practice
Calculus 1 -- Concavity; second derivative test -- Overview
Second Derivative Test
Calculus 1 -- Concavity; second derivative test -- Practice
Calculus 1: Lecture 3.4 Concavity and The Second Derivative Test
Connecting f, f', and f'' graphically | AP Calculus AB | Khan Academy
Mathematics P1 Nov 2005/ Grade 12 Final revision ( tricks and techniques)!@ zamokuhlemakhamba
Find the intervals of concavity from the derivative graph
Calculus I: Finding Intervals of Concavity and Inflection point
Calculus 1: Concavity Examples
Concavity | Calculus Lesson 24 - JK Math
Inflection point grade 12
Calculus 1. Section 3.4a Concavity and Second Derivative
Second derivative test | Using derivatives to analyze functions | AP Calculus AB | Khan Academy
Concavity Grade 12
How to Find Concavity in Calculus : Calculus Explained
Learn how to determine concavity and point of inflection AP style
Concavity Inflection Second Derivative Test 4 Examples Calculus 1 AB
Calculus 1 Lecture 3.1: Increasing/Decreasing and Concavity of Functions
Given fx sketch the first and second derivative graph
Calculus 1, Session 24 -- Concave up/down; inflection points; second derivative test
How to use the Second Derivative Test | Calculus 1
Комментарии
 0:12:49
0:12:49
 0:36:50
0:36:50
 1:43:31
1:43:31
 0:24:14
0:24:14
 0:12:48
0:12:48
 0:49:34
0:49:34
 1:27:51
1:27:51
 0:05:36
0:05:36
 6:17:03
6:17:03
 0:02:03
0:02:03
 0:04:21
0:04:21
 0:08:06
0:08:06
 0:19:49
0:19:49
 0:00:30
0:00:30
 0:29:06
0:29:06
 0:06:12
0:06:12
 0:00:53
0:00:53
 0:04:13
0:04:13
 0:06:34
0:06:34
 0:52:49
0:52:49
 1:34:07
1:34:07
 0:04:09
0:04:09
 1:14:00
1:14:00
 0:09:40
0:09:40